校内赛的题解还是不公开了。
代码的话……看难度而定。
时间似乎是乱序的。
在退役之前会高强度更新。
Vim 好像不支持自动生成目录,所以麻烦全文查找一下。
【来源未知】排列计数
请统计长为 的排列中,有多少组排列有至少 个位置满足 ,输出答案在 意义下的值。
【来源未知】排列计数 解法
正难则反。 考虑不合法的方案。
容易发现原命题的等价命题为 有多少排列有小于等于 n-4 个位置相同,逆命题为 有多少排列有大于 n-4 位相同,这个容易算。
- 恰好有 位相同的排列:。
- 恰好有 位相同的排列:。
- 恰好有 位相同的排列:。(因为 )
- 恰好有 位相同的排列:。
所以答案就是 。
代码难看。
#include <stdio.h>
const int maxn = 1e6, mod = 998244353;
int n, jn = 1;
const int inv2 = 499122177, inv3 = 332748118;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
jn = 1ll * jn * i % mod;
printf("%d", ((jn + mod - 2ll * n * (n - 1) % mod * (n - 2) % mod * inv2 % mod * inv3 % mod) % mod + mod - 1ll * n * (n - 1) % mod * inv2 % mod - 1) % mod);
return 0;
}
CF733E Sleep in class
有一个长度为n的楼梯,每节台阶上有一个字符串
- 为
U则代表向上走 - 为
D则代表向下走 - 当走过这个台阶后,台阶上的字符串会从U变为D或从D变成U
求从第个台阶开始要走出这N个台阶需要的步数(即从1号台阶向下,或N号台阶向上)
若出不去则输出
CF733E Sleep in class 解法
这个是模拟赛 T1,状况频出的一道题。 数组开小,压行 UB。 开大之后发现倍增空间炸了,然后发现不用倍增,输麻了。
首先我们可以发现被修改的格子一定是连续的,且一定是向左找 R,向右找 L,所以可以写出本题的 代码。
i64 query(int x)
{
i64 res = 0;
int l = x, r = x, st = ops[x];
while (true)
{
if (st == 1)
do
r++;
while (ops[r] == st && r <= n);
else
do
l--;
while (ops[l] == st && l);
res += (r - l);
st ^= 1;
if (r == n + 1 or l == 0)
return res;
}
}
稍微优化一下:
i64 query(int x)
{
i64 res = 0;
int l = x, r = x, st = ops[x];
while (true)
{
if (st == 1)
r = mostrl[r];
else
l = mostlr[l];
res += r;
res -= l;
st ^= 1;
if (r == n + 1 or l == 0)
return res;
}
}
预处理这样:
cin >> n;
for (int i = 1; i <= n; i++)
cin >> ch,
ops[i] = (ch == 'R');
ops[0] = ('R' == 'R');
ops[n + 1] = ('L' == 'R');
int p = n + 1;
for (int i = n; i; i--)
{
mostrl[i] = p;
if (ops[i] == 0)
p = i;
}
p = 0;
for (int i = 1; i <= n; i++)
{
mostlr[i] = p;
if (ops[i] == 1)
p = i;
}
我们就发现了实际上我们在找这个跳跃次数,然后求和左右端点。
所以我们可以得到跳跃次数,前缀和即可。 然后左右端点求和也是前缀和二分,不能倍增,要是开 256 就炸空间了。
i64 query(int x)
{
i64 steps[2] = {0, 0};
i64 res = 0;
steps[ops[x] ^ 1] = lsum[x + 1]; // getrstep(x);
steps[ops[x]] = rsum[x - 1]; // getlstep(x);
if ((ops[x] ^ (steps[0] > steps[1])))
res -= (n + 1);
steps[((steps[0] > steps[1]) ^ 1)] = steps[(steps[0] > steps[1])] - ((steps[0] > steps[1]) ^ 1);
if (ops[x])
res -= x;
else
res += x;
res -= gmostlrsum(x, steps[ops[x]]) * 2;
res += gmostrlsum(x, steps[ops[x] ^ 1]) * 2;
return res;
}
代码:
#include <iostream>
#include <string.h>
using std::cin;
using std::cout;
const char endl = '\n';
typedef long long i64;
const i64 mod = 1;
const int maxn = 5e5;
i64 ops[maxn], lsum[maxn], rsum[maxn];
i64 lisum[maxn], risum[maxn];
int n;
char ch;
int grsumsum(int l, int r) { return rsum[r] - rsum[l - 1]; }
i64 grisumsum(int l, int r) { return risum[r] - risum[l - 1]; }
int glsumsum(int l, int r) { return lsum[l] - lsum[r + 1]; }
i64 glisumsum(int l, int r) { return lisum[l] - lisum[r + 1]; }
i64 gbefksum(int x, int p)
{
if (p == 0)
return 0;
x--;
int l = 1, r = x;
if (grsumsum(1, x) < p)
{
return grisumsum(1, x);
}
while (r - l > 3)
{
int mid = (l + r) >> 1;
if (grsumsum(mid, x) > p)
l = mid;
else
r = mid;
}
for (int i = r; i >= l; i--)
if (grsumsum(i, x) == p)
{
return grisumsum(i, x);
}
return 0;
}
i64 gaftksum(int x, int p)
{
if (p == 0)
return 0;
x++;
int l = x, r = n;
if (glsumsum(x, n) < p)
{
return glisumsum(x, n) + (n + 1);
}
while (r - l > 3)
{
int mid = (l + r) >> 1;
if (glsumsum(x, mid) > p)
r = mid;
else
l = mid;
}
for (int i = l; i <= r; i++)
if (glsumsum(x, i) == p)
return glisumsum(x, i);
return -1;
}
i64 query(int x)
{
i64 steps[2] = {0, 0};
i64 res = 0;
steps[ops[x] ^ 1] = lsum[x + 1]; // getrstep(x);
steps[ops[x]] = rsum[x - 1]; // getlstep(x);
if ((ops[x] ^ (steps[0] > steps[1])))
res -= (n + 1);
steps[((steps[0] > steps[1]) ^ 1)] = steps[(steps[0] > steps[1])] - ((steps[0] > steps[1]) ^ 1);
if (ops[x])
res -= x;
else
res += x;
res -= gbefksum(x, steps[ops[x]]) * 2;
res += gaftksum(x, steps[ops[x] ^ 1]) * 2;
return res;
}
int main()
{
std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++)
cin >> ch,
ops[i] = (ch == 'U'),
lsum[i] = (ch == 'D'),
rsum[i] = (ch == 'U'),
lisum[i] = (ch == 'D') * i,
risum[i] = (ch == 'U') * i;
ops[0] = ('U' == 'U');
ops[n + 1] = ('D' == 'U');
rsum[0] = lsum[n + 1] = 1;
for (int i = 1; i <= n; i++)
rsum[i] += rsum[i - 1],
risum[i] += risum[i - 1];
for (int i = n; i >= 1; i--)
lsum[i] += lsum[i + 1],
lisum[i] += lisum[i + 1];
for (int i = 1; i <= n; i++)
cout << query(i) << ' ';
return 0;
}
P6327
给出一个长度为 的整数序列 ,进行 次操作,操作分为两类。
操作 :给出 ,将 分别加上 。
操作 :给出 ,询问 。
解法有两种,先给核心公式。
P6327 解法一
题解都是这个写法,不必我多言了吧。
P6327 解法二
这个标记是可以上推的,所以考虑线段树。
具体地,区间乘区间求和。
#include <bits/stdc++.h>
using namespace std;
#define mkpair make_pair
typedef long long i64;
typedef std::pair<int, int> pii;
typedef std::pair<i64, i64> pi64;
typedef std::vector<int> vint;
typedef std::vector<i64> vi64;
typedef std::queue<int> qint;
typedef std::queue<i64> qi64;
typedef std::priority_queue<int> pqint;
typedef std::priority_queue<i64> pqi64;
typedef long long i64;
const int maxn = 4.1e5;
typedef complex<double> cd;
cd tree[maxn << 2], lazy[maxn << 2];
inline cd initial(int u) { return cos(u) + 1.i * sin(u); }
int n, m, t, u, v, w;
void build(int index, int l, int r)
{
lazy[index] = 1.;
if (l == r)
{
cin >> u;
tree[index] = initial(u);
// cout << l << " : " << tree[index] << endl;
return;
}
int mid = (l + r) >> 1;
build(index << 1, l, mid),
build(index << 1 | 1, mid + 1, r);
tree[index] = tree[index << 1] + tree[index << 1 | 1];
// cout << l << " " << r << " : " << tree[index] << endl;
}
void setlazy(int index, int l, int r, cd val) { tree[index] *= val, lazy[index] *= val; }
void pushlazy(int index, int l, int r)
{
int mid = (l + r) >> 1;
setlazy(index << 1, l, mid, lazy[index]);
setlazy(index << 1 | 1, mid + 1, r, lazy[index]);
lazy[index] = 1.;
}
void modify(int index, int l, int r, int ql, int qr, cd val)
{
if (ql <= l and r <= qr)
{
// cout << "set " << index << " " << val << endl;
setlazy(index, l, r, val);
return;
}
if (l > qr or r < ql)
return;
pushlazy(index, l, r);
int mid = (l + r) >> 1;
modify(index << 1, l, mid, ql, qr, val),
modify(index << 1 | 1, mid + 1, r, ql, qr, val);
tree[index] = tree[index << 1] + tree[index << 1 | 1];
}
cd query(int index, int l, int r, int ql, int qr)
{
pushlazy(index, l, r);
if (ql <= l and r <= qr)
{
// cout << "ret " << l << " " << r << endl;
return tree[index];
}
if (l > qr or r < ql)
return 0;
int mid = (l + r) >> 1;
return query(index << 1, l, mid, ql, qr) +
query(index << 1 | 1, mid + 1, r, ql, qr);
}
int main()
{
// ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n;
build(1, 1, n);
cin >> m;
for (int i = 1; i <= m; i++)
{
cin >> t;
if (t == 1)
{
cin >> u >> v >> w;
// cout << "modify " << u << " " << v << " multiply " << initial(w) << endl;
modify(1, 1, n, u, v, initial(w));
// cout << "Not Supported!" << endl;
}
else
// cout << "query" << endl,
cin >> u >> v,
// cout << query(1, 1, n, u, v) << endl;
cout << fixed << setprecision(1) << query(1, 1, n, u, v).imag() << endl;
}
// cout << "end" << endl;
return 0;
}
abc323e Playlist
高桥有一个播放列表,里面有首歌。歌曲 持续秒。 Takahashi在时间开始随机播放播放列表。
随机播放重复以下内容:以等概率从首歌曲中选择一首歌,播放到最后。在这里,歌曲是连续播放的:一旦一首歌结束,下一首选择的歌曲立即开始。可以连续选择同一首歌。
求歌曲在时间后秒播放的概率,取的模。
abc323e Playlist 解法
看到这个就可以想到期望 dp 加背包了。 定义 为从第 秒开始播放,第 秒播放到第一首歌的概率。
我们便容易得到:
然后题就做完了。
int main()
{
cin >> n >> x;
invn = pow(n, mod - 2);
for (int i = 1; i <= n; i++)
cin >> v[i];
if (x < v[1])
{
cout << invn;
return 0;
}
for (int i = x; i > x - v[1]; i--)
f[i] = invn;
for (int i = x - 1; i >= 0; i--)
for (int j = 1; j <= n; j++)
f[i] = (1ll * f[i] + 1ll * f[i + v[j]] * invn) % mod;
cout << f[0];
return 0;
}
P4700 Traffic
在平面直角坐标系上有 个点,其中第 个点的坐标是 ,所有点在一个以 和 为相对顶点的矩形内。
如果 ,那么我们称这个点在西侧。如果 ,那么我们称这个点在东侧。
这些点之间有 条边,每条边可能是有向边也可能是无向边,保证边在交点以外的任何地方不相交。
现在请你求出,对于每一个西侧的点,能够沿着边到达多少东侧的点。
P4700 Traffic 解法
这道题最重要的性质就是:边保证在交点以外的任何地方不相交。
那我们得到如下性质:在去除了图中所有点不能到达的右侧点后,每个点能够到达的右侧点是一个区间。
我们考虑它的证明:假如存在左侧点 ,右侧点 ,使得 ,且 能够到达 ,对于每个右侧点,都存在一个左侧点可以到达。
则若有点要到达 ,就至少存在一条与 或 交叉的边,而边在交点外是不相交的,所以存在一个 或 路径上的交点,使得交点可以到达 。
由此得到:若一个左侧点能够到达 更高和更低的点,则中间的点也能到达。
所以我们只需要维护左侧点最高和最低的 值,这个的话缩点建反图然后 DAG dp 即可。
// Problem: P4700 [CEOI2011] Traffic
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4700
// Memory Limit: 125 MB
// Time Limit: 5000 ms
#include <algorithm>
#include <iostream>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <stack>
using std::cin;
using std::cout;
using std::max;
using std::min;
using std::vector;
// using std::endl;
const char endl = '\n';
typedef long long i64;
typedef std::pair<int, int> pii;
typedef std::vector<int> vint;
typedef std::queue<int> qint;
typedef std::map<int, int> mpii;
typedef std::stack<int> sint;
typedef long long i64;
const i64 mod = 1;
const int maxn = 4e5;
vint edge[maxn], edge_new_rev[maxn];
int flg[maxn], reach[maxn];
int scclo[maxn], scchi[maxn];
vector<pii> left, right, points;
mpii mping;
int n, m, r, _, u, v, w;
int dfn[maxn], low[maxn], cnt, scc[maxn], scnt, active[maxn], inscc[maxn];
sint st;
void tarjan(int index)
{
low[index] = dfn[index] = ++cnt;
st.push(index);
for (auto u : edge[index])
{
if (!dfn[u])
tarjan(u);
if (!scc[u])
low[index] = min(low[u], low[index]);
}
if (dfn[index] == low[index])
{
++scnt;
while (true)
{
int u = st.top();
st.pop();
scc[u] = scnt;
if (u == index)
break;
}
}
}
qint q;
const int inf = 1e9;
int main()
{
cin >> n >> m >> r >> _;
for (int i = 0; i < n; i++)
{
cin >> u >> v;
points.push_back({u, v});
if (u == 0)
left.push_back({-v, i});
}
for (int i = 1; i <= m; i++)
{
cin >> u >> v >> w, u--, v--,
edge[u].push_back(v);
if (w == 2)
edge[v].push_back(u);
}
for (auto x : left)
q.push(x.second);
sort(left.begin(), left.end());
while (!q.empty())
{
int u = q.front();
q.pop();
if (active[u])
continue;
active[u] = 1;
for (auto v : edge[u])
q.push(v);
}
for (int i = 0; i < n; i++)
if (active[i] and points[i].first == r)
right.push_back({points[i].second, i});
sort(right.begin(), right.end());
for (int i = 0, e = right.size(); i < e; i++)
mping[right[i].second] = i + 1;
for (int i = 0; i < n; i++)
if (!dfn[i])
tarjan(i);
for (int u = 0; u < n; u++)
for (auto v : edge[u])
if (scc[u] != scc[v])
edge_new_rev[scc[v]].push_back(scc[u]), inscc[scc[u]]++;
for (int i = 1; i <= scnt; i++)
scclo[i] = inf,
scchi[i] = -inf;
for (auto i : right)
scclo[scc[i.second]] = min(scclo[scc[i.second]], mping[i.second]);
for (auto i : right)
scchi[scc[i.second]] = max(scchi[scc[i.second]], mping[i.second]);
for (int i = 1; i <= scnt; i++)
if (!inscc[i])
q.push(i);
while (!q.empty())
{
int u = q.front();
q.pop();
for (auto x : edge_new_rev[u])
{
scclo[x] = min(scclo[u], scclo[x]),
scchi[x] = max(scchi[u], scchi[x]);
if (--inscc[x] == 0)
q.push(x);
}
}
for (auto i : left)
if (scchi[scc[i.second]] == -inf || scclo[scc[i.second]] == inf)
cout << 0 << endl;
else
cout << scchi[scc[i.second]] - scclo[scc[i.second]] + 1 << endl;
return 0;
}
P3343 地震后的幻想乡
傲娇少女幽香是一个很萌很萌的妹子,而且她非常非常地有爱心,很喜欢为幻想乡的人们做一些自己力所能及的事情来帮助他们。
这不,幻想乡突然发生了地震,所有的道路都崩塌了。现在的首要任务是尽快让幻想乡的交通体系重新建立起来。幻想乡一共有 个地方,那么最快的方法当然是修复 条道路将这 个地方都连接起来。 幻想乡这 个地方本来是连通的,一共有 条边。现在这 条边由于地震的关系,全部都毁坏掉了。每条边都有一个修复它需要花费的时间,第 条边所需要的时间为 。地震发生以后,由于幽香是一位人生经验丰富,见得多了的长者,她根据以前的经验,知道每次地震以后,每个 会是一个 到 之间均匀分布的随机实数。并且所有 都是完全独立的。
现在幽香要出发去帮忙修复道路了,她可以使用一个神奇的大魔法,能够选择需要的那 条边,同时开始修复,那么修复完成的时间就是这 条边的 的最大值。当然幽香会先使用一个更加神奇的大魔法来观察出每条边 的值,然后再选择完成时间最小的方案。 幽香在走之前,她想知道修复完成的时间的期望是多少呢?
P3343 地震后的幻想乡 解法
期望题,其实不需要积分,积分是为了证明最后的性质:
对于 个 之间的随机变量 ,第 小的那个的期望值是 。
这个性质最后来。
我们令 代表对于点集 的导出子图,在选择了 条边后仍然不连通的方案数量。
我们同时定义 为在 的条件下,图连通的方案数量。
定义 为 的导出子图中的边数,我们有 ,这是显然的。
然后我们就得到了本题的核心公式:
这里的 并没有被用到,但是为了保证不算重,是必要的,且对于相同的 ,应有相同的 。
我们强制 的子图 连通,然后选择 条边,这个图一定是不连通的。
然后枚举一下子集应该就完了。
最后的答案是这样的:
参考了这篇题解:题解 P3343 【[ZJOI2015]地震后的幻想乡】 - ButterflyDew 的博客 - 洛谷博客
#include <algorithm>
#include <iostream>
#include <iomanip>
#include <string.h>
#include <bitset>
#include <vector>
#include <string>
#include <queue>
#include <map>
#include <set>
using std::cin;
using std::cout;
using std::min;
// using std::endl;
const char endl = '\n';
typedef long long i64;
const int maxn = 11, maxm = 51;
std::vector<int> edge[maxn];
int n, m, u, v;
int lowbit(int set) { return set & (-set); }
i64 f[1 << maxn][maxm], C[maxm][maxm], g[1 << maxn][maxm];
int d[1 << maxn], graph[1 << maxn];
int main()
{
cin >> n >> m;
C[0][0] = 1;
for (int i = 1; i <= m; i++)
C[i][0] = 1;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= i; j++)
C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
for (int i = 0; i < m; i++)
cin >> u >> v, u--, v--,
graph[(1 << u) | (1 << v)]++;
for (int S = 1; S < (1 << n); S++)
for (int T = S; T; T = (T - 1) & S)
d[S] += graph[T];
for (int S = 1; S < (1 << n); S++) // enumerate S
for (int j = 0; j <= d[S]; j++)
{
for (int T = (S - 1) & S; T; T = (T - 1) & S) // T \subsetneq S
if (lowbit(S) & T) // k = lowbit(s) \in T
for (int u = 0; u <= min(j, d[T]); u++)
f[S][j] += g[T][u] * C[d[S ^ T]][j - u];
g[S][j] = C[d[S]][j] - f[S][j];
}
double s = 0;
for (int i = 0; i <= m; i++)
s += 1. * f[(1 << n) - 1][i] / C[m][i];
cout << std::fixed << std::setprecision(6) << (s / (1. + m));
return 0;
}
P2865 Roadblocks G
贝茜把家搬到了一个小农场,但她常常回到 FJ 的农场去拜访她的朋友。贝茜很喜欢路边的风景,不想那么快地结束她的旅途,于是她每次回农场,都会选择第二短的路径,而不象我们所习惯的那样,选择最短路。
贝茜所在的乡村有 条双向道路,每条路都连接了所有的 个农场中的某两个。贝茜居住在农场 ,她的朋友们居住在农场(即贝茜每次旅行的目的地)。
贝茜选择的第二短的路径中,可以包含任何一条在最短路中出现的道路,并且一条路可以重复走多次。当然第二短路的长度必须严格大于最短路(可能有多条)的长度,但它的长度必须不大于所有除最短路外的路径的长度。
P2865 Roadblocks G 解法
考虑答案必定是 u 到 v 的最短路的一条路径更改一条边得到的,所以处理出从 1 开始的最短路,从 n 开始的最短路,最后合并求解即可。
#include<stdio.h>
#include<queue>
#include<vector>
const int maxn = 1e5;
int n,m,u,v,w;
std::vector<std::pair<int,int> > edge[maxn];
std::priority_queue<std::pair<int,int> > q;
std::priority_queue<int> mins;
int dis[maxn],dis2[maxn],vis[maxn],mx;
void rundij(int* arr,int index){
for(int i=1;i<=n;i++)vis[i]=0,arr[i]=0x3f3f3f3f;
while(!q.empty())q.pop();
arr[index]=0,q.push({0,index});
while(!q.empty()){
auto u = q.top();q.pop();
if(vis[u.second])continue;vis[u.second]=1;
for(auto v:edge[u.second]){
if(arr[v.first] > arr[u.second] + v.second) arr[v.first] = arr[u.second] + v.second , q.push({-arr[v.first],v.first});
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&u,&v,&w),
edge[u].push_back({v,w}),
edge[v].push_back({u,w});
rundij(dis,1);
rundij(dis2,n);
for(int i=1;i<=n;i++)
for(auto u:edge[i])
{
int v = dis[i]+u.second+dis2[u.first];
if(v > dis[n])
mins.push(-v);
}
printf("%d",-mins.top());
return 0;
}
P3166 数三角形
给定一个 的网格,请计算三点都在格点上的三角形共有多少个。注意三角形的三点不能共线。
P3166 数三角形 解法
首先正难则反,考虑用总方案数减去三点共线的方案数。
然后我们发现我们需要求如下的一个东西:
给定两点 ,假定 ,求在这条线段上有多少个整点。
我们这样考虑:
将线段看作向量,那么这个向量可以转化为几个(斜率与原向量相同)向量的和。
起始点和终点都保证是整点,那么如果我们能将 变为两个向量 和 ,且这两个向量的横向分量和纵向分量长度都为整数,则存在一个整点。
可以被拆分成多个向量,且拆分的极限应该是 组,所以在这之中有 个整数点(忽略右侧端点)。
所以我们枚举所有端点对,然后统计中间的端点,然后用总方案数减去即可。
但这样的复杂度是 的,还会有一些可能会算重的情况,考虑优化。
我们将枚举端点对变为枚举一个端点和 以及 ,尽管复杂度不变,但注意到如下基本事实:所有 相同的线段对答案的贡献是相同的,考虑有多少对这样的线段,设想一个 的矩形在 的矩形内移动,会有 对。
所以我们就得到了本题的 做法( 同阶)。
#include<stdio.h>
#include<algorithm>
typedef long long i64;
i64 n,m,tot;
i64 C3(i64 x){return x*(x-1)/2ll*(x-2)/3ll;}
i64 intg(i64 dx,i64 dy){return std::__gcd(dx,dy)-1;}
int main(){
scanf("%lld%lld",&n,&m),n++,m++;
tot += C3(n*m);
tot -= n*C3(m) + m*C3(n);
for(int di=1;di<=n;di++)
for(int dj=1;dj<=m;dj++)
tot -= 2ll* intg(di,dj) * (n-di)*(m-dj);
printf("%lld",tot);
return 0;
}
然后这道题有一个复杂度更优的做法(莫比乌斯反演):
上面高亮的式子求的实际上就是:
有如下基本事实成立:,所以我们可以将 转为 。
然后就是漫长枯燥的式子推导:
最后这题就做完了,复杂度是线性的。
#include<stdio.h>
#include<algorithm>
typedef long long i64;
const int maxn = 200000;
int check[maxn],prime[maxn],phi[maxn],cnt;
void ola_prime(){
phi[1]=1;
for(int i=2;i<maxn;i++){
if(!check[i])
phi[i] = i-1,
prime[++cnt] = i;
for(int j=1;j<=cnt and i*prime[j]<maxn;j++){
check[i*prime[j]]=1;
if(!(i%prime[j])){
phi[i*prime[j]] = phi[i]*prime[j];
break;
}
else
phi[i*prime[j]] = phi[i]*(prime[j]-1);
}
}
}
i64 n,m,tot;
i64 C3(i64 x){return x*(x-1)/2ll*(x-2)/3ll;}
i64 intg(i64 dx,i64 dy){return std::__gcd(dx,dy)-1;}
i64 cal(i64 x,i64 d){return (x/d)*x-d*(x/d)*(x/d+1ll)/2ll;}
int main(){
ola_prime();
scanf("%lld%lld",&n,&m),n++,m++;
tot += C3(n*m);
tot -= n*C3(m) + m*C3(n);
for(int d=1,e=n<m?n:m;d<=e;d++)
tot -= 2*phi[d]*cal(n,d)*cal(m,d);
tot += n*(n-1)*m*(m-1)/2ll;
printf("%lld",tot);
return 0;
}
P1129 矩阵游戏
小 Q 是一个非常聪明的孩子,除了国际象棋,他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个 黑白方阵进行(如同国际象棋一般,只是颜色是随意的)。每次可以对该矩阵进行两种操作:
- 行交换操作:选择矩阵的任意两行,交换这两行(即交换对应格子的颜色)。
- 列交换操作:选择矩阵的任意两列,交换这两列(即交换对应格子的颜色)。
游戏的目标,即通过若干次操作,使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
对于某些关卡,小 Q 百思不得其解,以致他开始怀疑这些关卡是不是根本就是无解的!于是小 Q 决定写一个程序来判断这些关卡是否有解。
P1129 矩阵游戏 解法
二分图匹配,原因在这里:
首先不难证得,交换只会交换行(或列)。
然后考虑匹配,一行能匹配一列当且仅当这一列中,该行所在的位置是黑格。
所以我们给行和列各开虚点,给黑格的行连向列,最后求解二分图匹配即可。
#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
#define int long long
const int maxn = 2 * 207 + 5, maxm = 2 * 5000 + 5, inf = 0x3f3f3f3f3f3f3f3f;
int n, m, tot=1, head[maxn], cur[maxn], ter[maxm], nxt[maxm], cap[maxm], dis[maxn];
void add(int u, int v, int w) {ter[++tot] = v, nxt[tot] = head[u], cap[tot] = w, head[u] = tot;}
void addedge(int u, int v, int w) {
// printf("%d %d %d\n",u,v,w);
add(u, v, w) , add(v, u, 0);
}
bool bfs(int s,int t) {
memset(dis, -1 , sizeof(dis));
std::queue<int> q;
q.push(s), dis[s] = 0, cur[s] = head[s];
while(!q.empty()) {
int fr = q.front(); q.pop();
for(int i = head[fr] ; i ; i = nxt[i]) {
int v = ter[i];
if(cap[i] && dis[v] == -1) {
dis[v] = dis[fr] + 1;
q.push(v);
cur[v] = head[v];
if(v==t)
return true;
}
}
}
return false;
}
int dfs(int u, int t, int flow) {
if(u == t) return flow;
int ans = 0;
for(int &i = cur[u] ; i && ans < flow ; i = nxt[i]) {
int v = ter[i];
if(cap[i] && dis[v] == dis[u] + 1) {
int x = dfs(v, t, std::min(cap[i], flow - ans));
if(!x) dis[x] = -1;
cap[i] -= x,cap[i^1] += x, ans += x;
}
}
return ans;
}
int dinic(int s, int t) {
int ans = 0, x;
while (bfs(s,t)) {
while(x = dfs(s,t,inf))
ans += x;
}
return ans;
}
int T, u, v, w, c, s, t;
int point_left(int index) { return n+index;}
int point_up (int index) { return index;}
signed main() {
scanf("%lld",&T);
while(T--){
scanf("%lld",&n);
memset(head,0,sizeof head);
memset(cur,0,sizeof cur);
memset(ter,0,sizeof ter);
memset(nxt,0,sizeof nxt);
memset(cap,0,sizeof cap);
memset(dis,0,sizeof dis);
s = 2*n+1,t = 2*n+2;
tot = 1;
for(int i=1;i<=n;i++)
head[i] = 0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf("%lld",&u);
if(u)
addedge(point_left(i),point_up(j),1);
}
}
for(int i=1;i<=n;i++)
addedge(s,point_left(i),1),
addedge(point_up(i),t,1);
int ans = dinic(s, t);
puts(ans == n ? "Yes" : "No");
}
return 0;
}
P2120 仓库建设
L 公司有 个工厂,由高到低分布在一座山上,工厂 在山顶,工厂 在山脚。
由于这座山处于高原内陆地区(干燥少雨),L公司一般把产品直接堆放在露天,以节省费用。突然有一天,L 公司的总裁 L 先生接到气象部门的电话,被告知三天之后将有一场暴雨,于是 L 先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。
由于地形的不同,在不同工厂建立仓库的费用可能是不同的。第 个工厂目前已有成品 件,在第 个工厂位置建立仓库的费用是 。
对于没有建立仓库的工厂,其产品应被运往其他的仓库进行储藏,而由于 L 公司产品的对外销售处设置在山脚的工厂 ,故产品只能往山下运(即只能运往编号更大的工厂的仓库),当然运送产品也是需要费用的,一件产品运送一个单位距离的费用是 。
假设建立的仓库容量都都是足够大的,可以容下所有的产品。你将得到以下数据:
- 工厂 距离工厂 的距离 (其中 )。
- 工厂 目前已有成品数量 。
- 在工厂 建立仓库的费用 。
请你帮助 L 公司寻找一个仓库建设的方案,使得总的费用(建造费用 + 运输费用)最小。
简化题意:
有 个点,每个点有一定量()的物资,现在要选择一些点,将所有物资通过向右移动的方式汇集到这些点中,选择点和向右移动单位物资均有代价,求最小代价。
P2120 仓库建设 解法
我们首先想一个 的 dp 式子。
注意到如下基本事实:若一个点建立了仓库,则前面的没有运输进仓库的点都会运输到这里,所以每个仓库的覆盖范围是一定的。
我们定义 为前 个地点的物品都能被安置,且 号点是最后一个仓库时的最小花费。
则我们可以得到(下文中的 指的是题目中的 ,即距离):
我们定义 ,则上面的式子就变成了这样:
这个基本就是斜率优化的板子了,我们假定存在 且 ,同时 优于 (即选 转移 比选 更大),那么我们就能列出不等式:
于是我们将问题抽象如下:平面上有 个点,坐标为 ,若对于 的两点,满足两点的斜率小于 ,则选择右侧的点是更优的。
这里可以用凸壳维护,因为不在凸壳上的点一定劣于凸壳上的点,下面是具体原因:
我们假设有 三点,满足 ,且 在凸壳上, 在凸壳以内。
假如此时 优于 ,则有 ,结合几何相关知识得 此时 优于 ,所以 对答案没有贡献。
配上一张很丑的图示:

假如此时 劣于 ,则同样有 此时 劣于 ,同时 劣于 , 对答案同样没有贡献。

综上, 对答案是没有贡献的,所以我们可以维护一个下凸壳,因为凸壳上的斜率单调递增,所以可以在上面二分最优决策点。
但这题有更好的性质: 单调递增,所以我们可以直接维护一个单调队列代表凸壳上边的斜率,在查找时直接弹出队尾斜率不合法的点即可,因为队尾若不合法,接下来也不可能合法。
还有一个要注意的点(hack 数据),就是 等于 的情况,若末尾有连续的 ,取其 值的最小值即可。
代码不长,重在理解。
#include<stdio.h>
typedef long long i64;
const int maxn = 1.2e6;
int n;
i64 d[maxn],p[maxn],c[maxn],f[maxn],q[maxn],r[maxn];
i64 min(i64 a,i64 b){ return a<b?a:b;}
i64 decx (int index) { return q[index];}
i64 decy (int index) { return f[index]+r[index];}
i64 maked(int i,int u) { return f[u] + d[i] * (q[i] - q[u]) - r[i] + r[u] + c[i];}
// back -> . . . . . . . . . <- front
int que[maxn],vfront,vback;
int size () { return vfront-vback;}
int front () { return que[vfront-1];}
int front2 () { return que[vfront-2];}
int back () { return que[vback];}
int back2 () { return que[vback+1];}
void push (int v) { que[vfront++]=v;}
void pop_front() { vfront--;}
void pop_back () { vback++;}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld%lld%lld",d+i,p+i,c+i);
for(int i=1;i<=n;i++) q[i] = p[i] + q[i-1];
for(int i=1;i<=n;i++) r[i] = d[i] * p[i] + r[i-1];
push(0);
for(int i=1;i<=n;i++){
while(
size()>=2 and
(decy(back2())-decy(back()))
<= d[i] * (decx(back2())-decx(back()))
)
pop_back();
f[i] = maked(i,back());
while(
size()>=2 and
(decy(front())-decy(front2())) * (decx(i)-decx(front()))
>= (decy(i)-decy(front())) * (decx(front()) - decx(front2()))
)
pop_front();
push(i);
}
i64 ans = f[n];
int x=n;
while(p[x]==0)
x--,ans=min(ans,f[x]);
printf("%lld",ans);
return 0;
}
U121015 区间
(我小改了下题面)
给定 和 个数 ,求随机选择一段区间,区间的平均值在 到 之间的期望在 意义下的值。
U121015 区间 解法
首先将期望转化为方案数除总方案数,这步不用说。
我们发现如下性质:
定义 ,,则上面的式子就可以转化为:
就变成了一个逆序对问题,所以使用树状数组或逆序对即可。
P7453 大魔法师
大魔法师小 L 制作了 个魔力水晶球,每个水晶球有水、火、土三个属性的能量值。小 L 把这 个水晶球在地上从前向后排成一行,然后开始今天的魔法表演。
我们用 分别表示从前向后第 个水晶球(下标从 开始)的水、火、土的能量值。
小 L 计划施展 次魔法。每次,他会选择一个区间 ,然后施展以下 大类、 种魔法之一:
-
魔力激发:令区间里每个水晶球中特定属性的能量爆发,从而使另一个特定属性的能量增强。具体来说,有以下三种可能的表现形式:
- 火元素激发水元素能量:令 。
- 土元素激发火元素能量:令 。
- 水元素激发土元素能量:令 。
需要注意的是,增强一种属性的能量并不会改变另一种属性的能量,例如 并不会使 增加或减少。
-
魔力增强:小 L 挥舞法杖,消耗自身 点法力值,来改变区间里每个水晶球的特定属性的能量。具体来说,有以下三种可能的表现形式:
- 火元素能量定值增强:令 。
- 水元素能量翻倍增强:令 。
- 土元素能量吸收融合:令 。
-
魔力释放:小L将区间里所有水晶球的能量聚集在一起,融合成一个新的水晶球,然后送给场外观众。生成的水晶球每种属性的能量值等于区间内所有水晶球对应能量值的代数和。需要注意的是,魔力释放的过程不会真正改变区间内水晶球的能量。
值得一提的是,小 L 制造和融合的水晶球的原材料都是定制版的 OI 工厂水晶,所以这些水晶球有一个能量阈值 。当水晶球中某种属性的能量值大于等于这个阈值时,能量值会自动对阈值取模,从而避免水晶球爆炸。
小 W 为小 L(唯一的)观众,围观了整个表演,并且收到了小 L 在表演中融合的每个水晶球。小 W 想知道,这些水晶球蕴涵的三种属性的能量值分别是多少。
P7453 大魔法师 解法
考虑将这些都写成矩阵变换的形式,然后区间乘,维护区间和即可。
代码为线段树,通过展开矩阵乘法加速(不卡过不去,我常数太大了)。
// Problem: P7453 [THUSCH2017] 大魔法师
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7453
// Memory Limit: 500 MB
// Time Limit: 5000 ms
#include<stdio.h>
#include<ctype.h>
inline int read()
{
char c=getchar();int x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;return x;
}
const int mod = 998244353;
const int maxl = 4;
struct matrix{
int data[maxl][maxl];
int* operator[](int index){return data[index];}
matrix() { for(int i=0;i<maxl;i++)for(int j=0;j<maxl;j++)data[i][j] = 0;}
};
bool operator==(matrix a,matrix b){
for(int i=0;i<maxl;i++)
for(int j=0;j<maxl;j++)
if(a[i][j] != b[i][j])
return false;
return true;
}
matrix operator+(matrix a,matrix b){
matrix res;
for(int i=0;i<maxl;i++)
for(int j=0;j<maxl;j++)
res[i][j] = (a[i][j]+b[i][j])>=mod ? (a[i][j]+b[i][j]-mod) : (a[i][j]+b[i][j]);
return res;
}
matrix operator*(matrix a,matrix b){
matrix res;
res[0][0] = (1ll * a[0][1] * b[1][0] + 1ll * a[0][0] * b[0][0] + 1ll * a[0][2] * b[2][0] + 1ll * a[0][3] * b[3][0]) % mod;
res[0][1] = (1ll * a[0][0] * b[0][1] + 1ll * a[0][2] * b[2][1] + 1ll * a[0][1] * b[1][1] + 1ll * a[0][3] * b[3][1]) % mod;
res[0][2] = (1ll * a[0][0] * b[0][2] + 1ll * a[0][1] * b[1][2] + 1ll * a[0][2] * b[2][2] + 1ll * a[0][3] * b[3][2]) % mod;
res[0][3] = (1ll * a[0][0] * b[0][3] + 1ll * a[0][1] * b[1][3] + 1ll * a[0][2] * b[2][3] + 1ll * a[0][3] * b[3][3]) % mod;
res[1][0] = (1ll * a[1][0] * b[0][0] + 1ll * a[1][1] * b[1][0] + 1ll * a[1][2] * b[2][0] + 1ll * a[1][3] * b[3][0]) % mod;
res[1][1] = (1ll * a[1][0] * b[0][1] + 1ll * a[1][1] * b[1][1] + 1ll * a[1][2] * b[2][1] + 1ll * a[1][3] * b[3][1]) % mod;
res[1][2] = (1ll * a[1][0] * b[0][2] + 1ll * a[1][1] * b[1][2] + 1ll * a[1][2] * b[2][2] + 1ll * a[1][3] * b[3][2]) % mod;
res[1][3] = (1ll * a[1][0] * b[0][3] + 1ll * a[1][1] * b[1][3] + 1ll * a[1][2] * b[2][3] + 1ll * a[1][3] * b[3][3]) % mod;
res[2][0] = (1ll * a[2][0] * b[0][0] + 1ll * a[2][1] * b[1][0] + 1ll * a[2][2] * b[2][0] + 1ll * a[2][3] * b[3][0]) % mod;
res[2][1] = (1ll * a[2][0] * b[0][1] + 1ll * a[2][1] * b[1][1] + 1ll * a[2][2] * b[2][1] + 1ll * a[2][3] * b[3][1]) % mod;
res[2][2] = (1ll * a[2][0] * b[0][2] + 1ll * a[2][1] * b[1][2] + 1ll * a[2][2] * b[2][2] + 1ll * a[2][3] * b[3][2]) % mod;
res[2][3] = (1ll * a[2][0] * b[0][3] + 1ll * a[2][1] * b[1][3] + 1ll * a[2][2] * b[2][3] + 1ll * a[2][3] * b[3][3]) % mod;
res[3][0] = (1ll * a[3][0] * b[0][0] + 1ll * a[3][1] * b[1][0] + 1ll * a[3][2] * b[2][0] + 1ll * a[3][3] * b[3][0]) % mod;
res[3][1] = (1ll * a[3][0] * b[0][1] + 1ll * a[3][1] * b[1][1] + 1ll * a[3][2] * b[2][1] + 1ll * a[3][3] * b[3][1]) % mod;
res[3][2] = (1ll * a[3][0] * b[0][2] + 1ll * a[3][1] * b[1][2] + 1ll * a[3][2] * b[2][2] + 1ll * a[3][3] * b[3][2]) % mod;
res[3][3] = (1ll * a[3][0] * b[0][3] + 1ll * a[3][1] * b[1][3] + 1ll * a[3][2] * b[2][3] + 1ll * a[3][3] * b[3][3]) % mod;
return res;
}
namespace typed{
matrix add_unit,mul_unit,fire_splash,soil_splash,water_splash;
inline void init_matrix(){
mul_unit[0][0] = mul_unit[1][1] = mul_unit[2][2] = mul_unit[3][3] =
fire_splash[0][0] = fire_splash[0][1] = fire_splash[1][1] = fire_splash[2][2] = fire_splash[3][3] =
soil_splash[0][0] = soil_splash[1][1] = soil_splash[1][2] = soil_splash[2][2] = soil_splash[3][3] =
water_splash[0][0] = water_splash[1][1] = water_splash[2][0] = water_splash[2][2] = water_splash[3][3] = 1;
}
inline matrix ball(int a,int b,int c){
matrix res;
res[0][0] = a, res[1][0] = b, res[2][0] = c, res[3][0] = 1;
return res;
}
inline matrix fire_enchant(int v){
matrix res;
res[0][0] = res[1][1] = res[2][2] = res[3][3] = 1, res[0][3] = v;
return res;
}
inline matrix water_enchant(int v){
matrix res;
res[1][1] = v;
res[0][0] = res[2][2] = res[3][3] = 1;
return res;
}
inline matrix soil_enchant(int v){
matrix res;
res[2][3] = v;
res[0][0] = res[1][1] = res[3][3] = 1;
return res;
}
}
namespace segtree{
const int maxn = 1.1e6;
int a,b,c;
matrix data[maxn],lazy[maxn];
inline void init(int index,int l,int r){
lazy[index] = typed::mul_unit;
if(l==r){
a=read(),b=read(),c=read();
data[index] = typed::ball(a,b,c);
return;
}
int mid = (l+r)>>1;
init(index<<1,l,mid),init(index<<1|1,mid+1,r);
data[index] = data[index<<1] + data[index<<1|1];
}
inline void setlazy(int index,matrix v){
data[index] = v * data[index];
lazy[index] = v * lazy[index];
}
inline void pushdown(int index){
if(lazy[index] == typed::mul_unit)
return;
setlazy(index<<1,lazy[index]),setlazy(index<<1|1,lazy[index]);
lazy[index] = typed::mul_unit;
}
inline void mul(int index,int l,int r,int ql,int qr,matrix val){
pushdown(index);
if(ql <= l and r <= qr){
setlazy(index,val);
return;
}
if(l>qr or r<ql)
return;
int mid = (l+r)>>1;
mul(index<<1,l,mid,ql,qr,val),mul(index<<1|1,mid+1,r,ql,qr,val);
data[index] = data[index<<1] + data[index<<1|1];
}
inline matrix query(int index,int l,int r,int ql,int qr){
pushdown(index);
if(ql <= l and r <= qr)
return data[index];
if(l>qr or r<ql)
return typed::add_unit;
int mid = (l+r)>>1;
return query(index<<1,l,mid,ql,qr)+query(index<<1|1,mid+1,r,ql,qr);
}
}
using segtree::init;
using segtree::mul;
using segtree::query;
int n,m,u,v,w,c;
int main(){
typed::init_matrix();
n=read();
init(1,1,n);
m=read();
for(int i=1;i<=m;i++){
u=read();
if(u==1)
v=read(),w=read(),
mul(1,1,n,v,w,typed::fire_splash);
else if(u==2)
v=read(),w=read(),
mul(1,1,n,v,w,typed::soil_splash);
else if(u==3)
v=read(),w=read(),
mul(1,1,n,v,w,typed::water_splash);
else if(u==4)
v=read(),w=read(),c=read(),
mul(1,1,n,v,w,typed::fire_enchant(c));
else if(u==5)
v=read(),w=read(),c=read(),
mul(1,1,n,v,w,typed::water_enchant(c));
else if(u==6)
v=read(),w=read(),c=read(),
mul(1,1,n,v,w,typed::soil_enchant(c));
else if(u==7){
v=read(),w=read();
matrix res = query(1,1,n,v,w);
printf("%d %d %d\n",res[0][0],res[1][0],res[2][0]);
}
}
return 0;
}
P2922 Secret Message
贝茜正在领导奶牛们逃跑.为了联络,奶牛们互相发送秘密信息.
信息是二进制的,共有 ()条,反间谍能力很强的约翰已经部分拦截了这些信息,知道了第 条二进制信息的前 ()位,他同时知道,奶牛使用 ()条暗号.但是,他仅仅知道第 条暗号的前 ()位。
对于每条暗号 ,他想知道有多少截得的信息能够和它匹配。也就是说,有多少信息和这条暗号有着相同的前缀。当然,这个前缀长度必须等于暗号和那条信息长度的较小者。
在输入文件中,位的总数(即 )不会超过 。
P2922 Secret Message 解法
看到这题就应该拍一个字典树上去,有两种情况存在:
- 当前字符串是某串的前缀
- 某串是当前字符串的前缀
无脑开树,路径上查询有多少个结尾,最后查询子树和即可。
// Problem: P2922 [USACO08DEC] Secret Message G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2922
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include<stdio.h>
const int maxn = 1.2*500000;
int sons[maxn][2],cnt=1,tag[maxn],sum[maxn];
void build(){
int size,val,index=1;
scanf("%d",&size);
for(int i=0;i<size;i++){
scanf("%d",&val);
if(!sons[index][val])
// printf("create %d\n",cnt+1),
sons[index][val] = ++cnt;
index = sons[index][val];
sum[index]++;
}
tag[index]++;
sum[index]--;
}
int query(){
int size=0,val=0,index=1,res=0;
scanf("%d",&size);
for(int i=0;i<size;i++){
scanf("%d",&val);
// printf("add tag_%d\n",index);
index = sons[index][val];
res += tag[index];
}
// res += sum[sons[index][0]] + sum[sons[index][1]];
return res + sum[index];
}
int n,m;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
build();
for(int i=1;i<=m;i++)
printf("%d\n",query());
return 0;
}
P4824 Censoring S
Farmer John为他的奶牛们订阅了Good Hooveskeeping杂志,因此他们在谷仓等待挤奶期间,可以有足够的文章可供阅读。不幸的是,最新一期的文章包含一篇关于如何烹制完美牛排的不恰当的文章,FJ不愿让他的奶牛们看到这些内容。
FJ已经根据杂志的所有文字,创建了一个字符串 ( 的长度保证不超过 ),他想删除其中的子串 ,他将删去 中第一次出现的子串 ,然后不断重复这一过程,直到 中不存在子串 。
注意:每次删除一个子串后,可能会出现一个新的子串 (说白了就是删除之后,两端的字符串有可能会拼接出来一个新的子串 )。
P4824 Censoring S 解法
之前就认为是神题的神题。
考虑 KMP 匹配,主要去考虑删除怎么做。
在删除之后,如果我们要继续匹配,那么就需要将匹配恢复到之前的状态。
现在关键就在于这个记录状态和删除状态的过程。
我们不能回退指针,这样会让复杂度假掉,考虑记录 kmp 的匹配栈,在匹配到时弹掉。
匹配栈应该是用于记录第二指针的位置的。
然后维护第二个栈用于存放答案,找到就在两个栈中弹出匹配到的部分,这题就做完了,但是用STL记得判空!
// Problem: P4824 [USACO15FEB] Censoring S
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4824
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include<stdio.h>
#include<string.h>
#include<stack>
const int maxn = 3e6;
char str[maxn],fnd[maxn];
int nxt[maxn];
int sl,fl,ps,pf;
std::stack<int> matches;
std::stack<char> result,re2;
int main(){
scanf("%s%s",str,fnd);
sl = strlen(str);
fl = strlen(fnd);
ps=0,pf=-1;
nxt[0]=-1;
while(ps<fl){
if(pf==-1 or fnd[ps] == fnd[pf])
nxt[++ps] = ++pf;
else
pf = nxt[pf];
}
ps=0,pf=0;
while(ps<sl){
if(pf==-1 or str[ps] == fnd[pf])
result.push(str[ps]),matches.push(++pf),ps++;
else
pf = nxt[pf];
if(pf == fl){
for(int i=0;i<fl;i++) matches.pop(),result.pop();
if(!matches.empty())
pf = matches.top();
else
pf = 0;
}
}
while(!result.empty())
re2.push(result.top()),
result.pop();
while(!re2.empty())
putchar(re2.top()),
re2.pop();
return 0;
}
CF 1883E
给定长度为 的序列 ,你可以进行以下操作。
选取一个 满足 ,使 变为原来的 倍。
求最少需要几次操作使得 为一个不下降的序列。
CF 1883E 解法
最优的策略一定是从左到右扫,但是乘可能一定会炸存储范围。
那这里我们可以用一个好玩的 trick,忘了哪里看到的了。
有如下基本事实成立:
所以你可以把所有数 了再做,但直接做的话会被卡精度,然后我卡不过去。
所以这里你开一个分数类将数字拆成相对大小和零头,比如 ,然后再做就很简单了(对数到底数大于 实数的映射也是单增的),注意零头带来的边界条件。
struct frac{
i64 a, b;
void simplize(){
i64 g = std::__gcd(a, b);
a/=g, b/=g;
}
frac(i64 a_ = 0, i64 b_ = 1) : a(a_), b(b_) { simplize(); }
bool m2() { return a < 2*b; }
void d2() { b *= 2; }
};
bool operator== (frac a, frac b) {
return a.a * b.b == a.b * b.a;
}
bool operator> (frac a, frac b) { return a.a * b.b > a.b * b.a; }
const int maxn = 3e5;
int n;
vint ve, re;
frac fs[maxn];
double mx;
long long ans = 0;
typedef long long i64;
void solve(){
ans = 0;
cin >>n;
in_vec(ve, n);
to_siz(re, n);
array(ve);
for(int i=0;i<ve.size();i++){
fs[i] = frac(ve[i]);
while(not fs[i].m2()) { fs[i].d2();re[i]++; }
fs[i].simplize();
if(i==0)
continue;
if(re[i-1] >= re[i]){
int delta = (re[i-1] - re[i]) + (fs[i-1] > fs[i]);
re[i] += delta;
ans += delta;
}
}
cout << ans << endl;
}
CF1883F You Are So Beautiful
给定数列 ,定义一个子序列 是合法的当且仅当从 中有且仅有一种选法能选出子序列 (选法相同定义为最终选出的位置集合相同)。
求其有多少非空合法子序列,满足它占据了 中一端连续的区间。
。
CF1883F You Are So Beautiful 解法
有如下基本事实成立:
若选择一段区间,第一个数在原数列是第一次出现,最后一个数在原数列是最后一次出现,则这段区间在原数列唯一。
所以开桶扫一扫就行了。
int n;
vint li, fr, ls;
std::map<int,int> las;
void solve(){
las.clear();
cin >> n;
in_vec(li,n);
to_siz(fr,n);
to_siz(ls,n);
for(int i=0;i<n;i++)
fr[i] = !las.count(li[i]),
las[li[i]]=i;
for(int i=0;i<n;i++)
ls[i] = (las[li[i]] == i);
for(int i=1;i<n;i++)
fr[i] += fr[i-1];
i64 ans=0;
for(int i=n-1;i>=0;i--)
ans += fr[i]*ls[i];
cout << ans << endl;
// array(fr);
// array(ls);
}
CF 1883G1 Dances (Easy version)
CF 1883G1 Dances (Easy version) 解法
我的思路是尺取,正解是二分答案,那就两个都讲。 两个解法基于一个相同的假定:排序数组,删除一定删 的最大值和 的最小值,这样一定是不劣的。
CF 1883G1 Dances (Easy version) 解法1 尺取
考虑数列处于如下一个情况:,这个情况是可以放缩的,也就是说 成立。
所以双指针一下,细节说不清楚,结合 ,答案为 模拟一下即可。
vint a, b;
int n, m;
void solve(){
cin >> n >> m;
in_vec(a, n-1);
a.push_back(m);
in_vec(b, n);
sort(a.begin(), a.end());
sort(b.begin(), b.end());
array(a); array(b);
int la=0, ra=n-1, lb=0, rb=n-1, ans = 0;
while(la <= ra){
if(a[ra] >= b[rb]){
ans ++;
if(rb+1<n)
rb++;
else
ra--,lb++;
}
else
ra--,rb--;
}
cout << ans << endl;
}
CF 1883G1 Dances (Easy version) 解法2 二分答案
二分删几个然后 检验即可。
int n, m;
vint i1, v1, v2;
bool check(int l1, int l2, int siz){
for(int i=0;i<siz;i++)
if(v1[l1+i] >= v2[l2+i])
return false;
return true;
}
int solve(int m){
to_siz(v1, n);
copy(i1.begin(), i1.end(), v1.begin());
v1[n-1] = m;
sort(v1.begin(), v1.end());
array(v1);
array(v2);
int l=0, r=n;
while(r-l>1){
int mid = (l+r)>>1;
if(check(0,mid,n-mid))
r = mid;
else
l = mid+1;
}
for(int i=l;i<=r;i++)
if(check(0,i,n-i)){
return i;
}
}
void solve(){
cin >> n >> m;
in_vec(i1, n-1);
in_vec(v2, n);
sort(v2.begin(), v2.end());
cout << solve(1) << endl;
}
CF1883G2 Dances (Hard Version)
对于每组数据,给定 , 与数组 的第 到 项和数组 的第 到 项。你需要根据 数组求出 个 数组的值,具体地:
对于每一个独立的 数组与互不影响的 ,你可以将 、 数组中的数字随意排序,再随意删除 与 中的 个数,对于每一个 数组,求最小的 使得 ,输出所有 的删除数 的和
CF1883G2 Dances (Hard Version) 解法
你现在已经会 1883G1 了。
然后你需要处理多组询问。
这个很简单的,假设答案关于第一个数字 的函数是 ,那么容易证明 。
说人话就是,第一个数对答案的影响至多有 ,然后你二分求得 即可。
如果用我尺取的思路似乎比正解快一个 。
int n, m;
vint v1, a, b;
int solve_ans(int spec){
to_siz(a, n);
copy(v1.begin(), v1.end(), a.begin());
a[n-1] = spec;
sort(a.begin(), a.end());
int la=0, ra=n-1, lb=0, rb=n-1, ans = 0;
while(la <= ra){
if(a[ra] >= b[rb]){
ans ++;
if(rb+1<n)
rb++;
else
ra--,lb++;
}
else
ra--,rb--;
}
return ans;
}
void solve(){
cin >> n >> m;
in_vec(v1, n-1);
in_vec(b, n);
sort(b.begin(), b.end());
int l=0, r=m; // find max l when f = 0
int initial = solve_ans(1);
while(r-l>1){
int mid = (l+r)>>1;
if(solve_ans(mid) - initial)
r = mid-1;
else
l = mid;
}
long long ans = 1ll * initial * m;
for(int i=r;i>=l;i--)
if(solve_ans(i) - initial == 0){
if(i>=m){
cout << ans << endl;
return;
}
ans = ans + m-i;
cout << ans << endl;
return;
}
}
int n, m;
vint i1, v1, v2;
bool check(int l1, int l2, int siz){
for(int i=0;i<siz;i++)
if(v1[l1+i] >= v2[l2+i])
return false;
return true;
}
int solve_ans(int m){
to_siz(v1, n);
copy(i1.begin(), i1.end(), v1.begin());
v1[n-1] = m;
sort(v1.begin(), v1.end());
array(v1);
array(v2);
int l=0, r=n;
while(r-l>1){
int mid = (l+r)>>1;
if(check(0,mid,n-mid))
r = mid;
else
l = mid+1;
}
for(int i=l;i<=r;i++)
if(check(0,i,n-i)){
return i;
}
}
void solve(){
cin >> n >> m;
in_vec(i1, n-1);
in_vec(v2, n);
sort(v2.begin(), v2.end());
int l=0, r=m; // find max l when f = 0
int initial = solve_ans(1);
while(r-l>1){
int mid = (l+r)>>1;
if(solve_ans(mid) - initial)
r = mid-1;
else
l = mid;
}
long long ans = 1ll * initial * m;
for(int i=r;i>=l;i--)
if(solve_ans(i) - initial == 0){
if(i>=m){
cout << ans << endl;
return;
}
ans = ans + m-i;
cout << ans << endl;
return;
}
}
P5018 对称二叉树
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
- 二叉树;
- 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 表示节点编号。
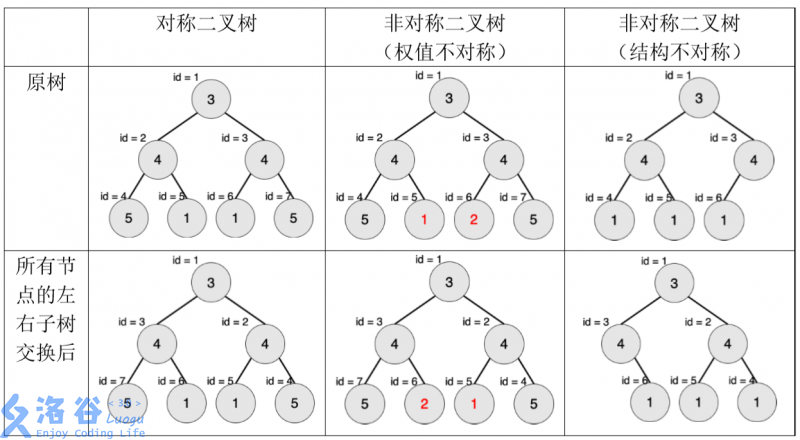
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 为子树根的一棵“子 树”指的是:节点 和它的全部后代节点构成的二叉树。
CF1883G2 Dances (Hard Version) 解法
乱搞做法。
hash 子树是肯定的。
考虑如下基本事实:矩阵乘法不满足交换律,所以用它来确定树的形态。
具体地,设定两个不同的矩阵 ,然后如下规定:
- 空树的 hash 为零矩阵
- 只有一个节点的树的 hash 为 。
- 对于其他所有树,其 hash 应为 。
最后就秒掉了。
// Problem: P5018 [NOIP2018 普及组] 对称二叉树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5018
// Memory Limit: 256 MB
// Time Limit: 1000 ms
#include<stdio.h>
#include<memory.h>
const int mod1 = 998244353, mod2 = 998244853;
const int maxl = 2, maxn = 1000007;
struct matrix{
int data1[maxl][maxl], data2[maxl][maxl];
matrix() { memset(data1,0,sizeof data1), memset(data2,0,sizeof data2); }
};
bool operator==(matrix a, matrix b){
for(int i=0;i<maxl;i++)
for(int j=0;j<maxl;j++)
if(a.data1[i][j] != b.data1[i][j] or a.data2[i][j] != b.data2[i][j])
return false;
return true;
}
matrix operator*(matrix a, matrix b){
matrix res;
for(int i=0;i<maxl;i++)
for(int j=0;j<maxl;j++)
for(int k=0;k<maxl;k++)
res.data1[i][j] = (1ll*res.data1[i][j] + 1ll*a.data1[i][k]*b.data1[k][j] )%mod1,
res.data2[i][j] = (1ll*res.data2[i][j] + 1ll*a.data2[i][k]*b.data2[k][j] )%mod2;
return res;
}
matrix operator+(matrix a, matrix b){
matrix res;
for(int i=0;i<maxl;i++)
for(int j=0;j<maxl;j++)
res.data1[i][j] = (res.data1[i][j] + a.data1[i][j] + b.data1[i][j]) %mod1,
res.data2[i][j] = (res.data2[i][j] + a.data2[i][j] + b.data2[i][j]) %mod2;
return res;
}
namespace typed{
matrix L,R,I;
void prework(){
L.data1[0][0] = L.data2[0][0] = 331;
L.data1[1][1] = L.data2[1][1] = 821;
L.data1[1][0] = L.data2[1][0] = 711;
L.data1[0][1] = L.data2[0][1] = 961;
R.data1[0][0] = R.data2[0][0] = 169;
R.data1[1][0] = R.data2[1][0] = 117;
R.data1[0][1] = R.data2[0][1] = 128;
R.data1[1][1] = R.data2[1][1] = 133;
I.data1[0][0] = I.data1[1][1] = I.data2[0][0] = I.data2[1][1] = 1;
}
}
matrix f[maxn],fr[maxn];
int ls[maxn], rs[maxn], v[maxn], size[maxn];
int npos = -1;
int n,mx;
void dfs(int index){
if(index == npos)
return;
size[index] = 1;
dfs(ls[index]);
dfs(rs[index]);
if(ls[index] != -1)
size[index] += size[ls[index]];
if(rs[index] != -1)
size[index] += size[rs[index]];
f [index].data1[0][0] = f [index].data1[1][1] = f [index].data2[0][0] = f [index].data2[1][1] = v[index];
fr[index].data1[0][0] = fr[index].data1[1][1] = fr[index].data2[0][0] = fr[index].data2[1][1] = v[index];
if(ls[index] != -1)
f [index] = f [index] + typed::L * f[ls[index]],
fr[index] = fr[index] + typed::R * fr[ls[index]];
if(rs[index] != -1)
f [index] = f [index] + typed::R * f[rs[index]],
fr[index] = fr[index] + typed::L * fr[rs[index]];
if(f[index] == fr[index]) mx = size[index] > mx ? size[index] : mx;
}
int main(){
typed::prework();
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",v+i);
for(int i=1;i<=n;i++)
scanf("%d%d",ls+i,rs+i);
dfs(1);
printf("%d",mx);
return 0;
}
P8085 KRIPTOGRAM
现有一段明文和一部分密文。明文和密文都由英文单词组成,且密文中的一个单词必然对应着明文中的一个单词。
求给出的密文在明文中可能出现的最早位置。
P8085 KRIPTOGRAM 解法
考虑“相同的内容相同,不同的内容不同”这条约束。
考虑一段区间,每个点的值都是距离自己最近的上一个相同串的距离,则可以解决这个问题。
然后就滑动窗口维护这个区间的 hash 即可。
烦人,快速幂写错了。
// Problem: P8085 [COCI2011-2012#4] KRIPTOGRAM
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8085
// Memory Limit: 128 MB
// Time Limit: 1000 ms
#include <algorithm>
#include <stdio.h>
#include <random>
#include <vector>
#include <queue>
#include <map>
const int mod1 = 998244353,
mod2 = 1000000007;
const int maxn = 1.2e6;
std::mt19937 gen(387961);
int lucky1[maxn], lucky2[maxn];
const int p1 = 387, p2 = 961;
const int g1 = 385, g2 = 633;
int pow1(int x,int p){ int res = 1; while(p){ if(p&1) res = 1ll * res * x % mod1; x = 1ll * x * x % mod1; p>>=1; } return res; }
int pow2(int x,int p){ int res = 1; while(p){ if(p&1) res = 1ll * res * x % mod2; x = 1ll * x * x % mod2; p>>=1; } return res; }
void ins(std::vector<std::pair<int,int>>& v){
int val1 = 0, val2 = 0;
char ch;
while(true){
ch = getchar();
if(ch == '\n' or ch == '\r')
continue;
if(ch == '$')
return;
else if(ch == ' ')
v.push_back({val1, val2}), val1 = 0, val2 = 0;
else
val1 = (1ll * val1 * p1 + lucky1[ch-'a']) % mod1,
val2 = (1ll * val2 * p2 + lucky2[ch-'a']) % mod2;
}
}
std::vector<std::pair<int,int>> v1, v2;
std::vector<int> l1, l2;
std::vector<int> fr1, fr2;
std::map<std::pair<int,int>, int> bucket;
int h11, h12, h21, h22;
void hash_initial(const std::vector<int>& ve, int lenn, int &h1, int& h2){
h1 = 0, h2 = 0;
for(int i=0; i<lenn; i++)
h1 = (1ll * h1 * g1 + mod1 + ve[i]) % mod1,
h2 = (1ll * h2 * g2 + mod2 + ve[i]) % mod2;
}
int main(){
for(int i=0;i<maxn;i++) lucky1[i] = gen() % mod1, lucky2[i] = gen() % mod2;
ins(v1), ins(v2);
bucket.clear(); for(int i=v1.size()-1; i>=0 ; i--) l1 .push_back(bucket.count(v1[i])?(bucket[v1[i]]-i):-1), bucket[v1[i]]=i; std::reverse(l1.begin(), l1.end());
bucket.clear(); for(int i=v2.size()-1; i>=0 ; i--) l2 .push_back(bucket.count(v2[i])?(bucket[v2[i]]-i):-1), bucket[v2[i]]=i; std::reverse(l2.begin(), l2.end());
bucket.clear(); for(int i=0 ; i<v1.size(); i++) fr1.push_back(bucket.count(v1[i])?(i-bucket[v1[i]]):-1), bucket[v1[i]]=i;
bucket.clear(); for(int i=0 ; i<v2.size(); i++) fr2.push_back(bucket.count(v2[i])?(i-bucket[v2[i]]):-1), bucket[v2[i]]=i;
hash_initial(fr1, fr2.size(), h11, h12);
hash_initial(fr2, fr2.size(), h21, h22);
for(int l=0, r=fr2.size(); r<fr1.size(); l++,r++){
if(h11 == h21 and h12 == h22) {
printf("%d\n", l+1);
return 0;
}
h11 = 1ll * h11 * g1 % mod1, h12 = 1ll * h12 * g2 % mod2;
if(l1[l]!=-1){
if(r-l-l1[l] >= 0)
h11 = (1ll * h11 + mod1 - 1ll * (fr1[l+l1[l]]+1) * pow1(g1, r-l-l1[l]) %mod1) % mod1,
h12 = (1ll * h12 + mod2 - 1ll * (fr1[l+l1[l]]+1) * pow2(g2, r-l-l1[l]) %mod2) % mod2;
fr1[l+l1[l]]=-1;
}
h11 = (1ll * h11 + 1ll * mod1 + 1ll * -fr1[l] * pow1(g1, r-l) %mod1) % mod1,
h12 = (1ll * h12 + 1ll * mod2 + 1ll * -fr1[l] * pow2(g2, r-l) %mod2) % mod2;
fr1[l]=0;
h11 = (1ll * h11 + mod1 + fr1[r]) % mod1,
h12 = (1ll * h12 + mod2 + fr1[r]) % mod2;
}
printf("no such match.\n");
return 0;
}
校内模拟赛 【数据删除】
原题不说,因为这道题太太太好玩了就放上来了!
你需要维护一个数据结构,见下。
校内模拟赛 【数据删除】 解法
权值线段树。
【数据删除】
【数据删除】
这个是一个小清新 ds(确切地,线段树)题,相当于要维护这些:
- 反转前 k 个 0 或 1
- 求出数列的二阶前缀和
首先我们来看二阶前缀和的式子( 为二阶前缀和数组, 为原数组):
因为我们要用线段树(确切地,权值线段树)维护,那么我们需要考虑二维前缀和应该如何合并。
也就是说,一个数列的二阶前缀和就是左半边的二阶前缀和加上右半边的二阶前缀和,最后加上右侧区间的长度乘上左侧的一阶前缀和。
struct Node {
int f1;
i64 f2;
int sons[2];
Node() {
f1 = f2 = 0;
sons[0] = sons[1] = 0;
}
} tree[maxn];
inline void update(int index, int l, int r) {
if (l == r)
return;
int mid = (l + r) >> 1;
int rlen = r - mid;
tree[index].f1 = (tree[tree[index].sons[0]].f1) + (tree[tree[index].sons[1]].f1);
tree[index].f2 = (tree[tree[index].sons[0]].f2) + (tree[tree[index].sons[1]].f2) +
1ll * rlen * tree[tree[index].sons[0]].f1;
}
请结合类型定义理解。
然后我们要反转这个玩意,有点复杂,具体地,将 0 反转成 1 实际上就是把左边的一段区间赋值为 1,反之亦然。
那我们其实是要找到从左边开始的包含 k 个 0 的连续区间,那就考虑权值线段树上二分。
什么, 空间不行?动态开点就是了,空间复杂度是 量级的。
这个写法比可能留下来的另一种线段树做法好想,不需要 lazy,还少存点东西。
这个是线段树上二分的板子:
// fill left ks 0 to 1
void fill0to1(int index, int l, int r, int k) {
if ((r - l + 1) - tree[index].f1 == k or l == r)
return fill1(index, l, r);
pushdown(index, l, r);
int mid = (l + r) >> 1;
int llen = (mid - l + 1);
int l0 = llen - tree[tree[index].sons[0]].f1; // count 0 in left subtree
if (l0 >= k)
fill0to1(tree[index].sons[0], l, mid, k);
else {
fill1(tree[index].sons[0], l, mid);
fill0to1(tree[index].sons[1], mid + 1, r, k - l0);
}
update(index, l, r);
}
// fill left ks 1 to 0
void fill1to0(int index, int l, int r, int k) {
if (tree[index].f1 == k or l == r)
return fill0(index, l, r);
pushdown(index, l, r);
int mid = (l + r) >> 1;
int llen = (mid - l + 1);
int l1 = tree[tree[index].sons[0]].f1;
if (l1 >= k)
fill1to0(tree[index].sons[0], l, mid, k);
else {
fill0(tree[index].sons[0], l, mid);
fill1to0(tree[index].sons[1], mid + 1, r, k - l1);
}
update(index, l, r);
}
最后再把它们拼起来就行了!
代码给两份,指针的容易懂,数组的快。
// array version
#include <stdio.h>
typedef long long i64;
#ifndef debug_rickyxrc
const int maxn = 6.2e7;
#else
const int maxn = 2000;
#endif
char Ed;
struct Node {
int f1;
i64 f2;
int sons[2];
Node() {
f1 = f2 = 0;
sons[0] = sons[1] = 0;
}
} tree[maxn];
char Bg;
int cnt = 1;
int newnode() { return ++cnt; }
inline void fill0(int index, int l, int r) {
tree[index].f1 = 0;
tree[index].f2 = 0;
tree[index].sons[0] = tree[index].sons[1] = 0;
}
inline void fill1(int index, int l, int r) {
tree[index].f1 = r - l + 1;
tree[index].f2 = (1ll + (r - l + 1)) * (r - l + 1) / 2;
tree[index].sons[0] = tree[index].sons[1] = 0;
}
inline void pushdown(int index, int l, int r) {
if (l == r)
return;
int mid = (l + r) >> 1;
if (not tree[index].sons[0]) {
tree[index].sons[0] = newnode();
if (tree[index].f1 == (r - l + 1))
fill1(tree[index].sons[0], l, mid);
}
if (not tree[index].sons[1]) {
tree[index].sons[1] = newnode();
if (tree[index].f1 == (r - l + 1))
fill1(tree[index].sons[1], mid + 1, r);
}
}
inline void update(int index, int l, int r) {
if (l == r)
return;
int mid = (l + r) >> 1;
int rlen = r - mid;
tree[index].f1 = (tree[tree[index].sons[0]].f1) + (tree[tree[index].sons[1]].f1);
tree[index].f2 = (tree[tree[index].sons[0]].f2) + (tree[tree[index].sons[1]].f2) +
1ll * rlen * tree[tree[index].sons[0]].f1;
}
// fill left ks 0 to 1
void fill0to1(int index, int l, int r, int k) {
if ((r - l + 1) - tree[index].f1 == k or l == r)
return fill1(index, l, r);
pushdown(index, l, r);
int mid = (l + r) >> 1;
int llen = (mid - l + 1);
int l0 = llen - tree[tree[index].sons[0]].f1; // count 0 in left subtree
if (l0 >= k)
fill0to1(tree[index].sons[0], l, mid, k);
else {
fill1(tree[index].sons[0], l, mid);
fill0to1(tree[index].sons[1], mid + 1, r, k - l0);
}
update(index, l, r);
}
// fill left ks 1 to 0
void fill1to0(int index, int l, int r, int k) {
if (tree[index].f1 == k or l == r)
return fill0(index, l, r);
pushdown(index, l, r);
int mid = (l + r) >> 1;
int llen = (mid - l + 1);
int l1 = tree[tree[index].sons[0]].f1;
if (l1 >= k)
fill1to0(tree[index].sons[0], l, mid, k);
else {
fill0(tree[index].sons[0], l, mid);
fill1to0(tree[index].sons[1], mid + 1, r, k - l1);
}
update(index, l, r);
}
i64 n, m, c;
int main() {
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Mem usage: %.4lf KB\n", (&Ed - &Bg) / 1024.0);
fprintf(stderr, "Mem usage: %.4lf MB\n", (&Ed - &Bg) / 1024.0 / 1024.0);
#endif
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%lld", &c);
if (c > 0)
fill0to1(1, 1, n, c);
if (c < 0)
fill1to0(1, 1, n, -c);
printf("%lld\n", tree[1].f2);
}
return 0;
}
// pointer version
#include<stdio.h>
typedef long long i64;
#ifndef debug_rickyxrc
const int maxn = 2.15e7;
#else
const int maxn = 2000;
#endif
char Ed;
struct Node{
int f1; i64 f2;
Node* sons[2];
Node() { f1 = f2 = 0; sons[0] = sons[1] = nullptr; }
~Node() {
if(sons[0] == nullptr) delete sons[0];
if(sons[1] == nullptr) delete sons[1];
}
} *root = new Node;
char Bg;
int cnt = 1;
// int newnode() {return ++cnt;}
inline void fill0(Node* index, int l, int r) {
index->f1 = 0; index->f2 = 0;
index->sons[0] = index->sons[1] = nullptr;
}
inline void fill1(Node* index, int l, int r) {
index->f1 = r-l+1; index->f2 = (1ll + (r-l+1)) * (r-l+1) / 2;
index->sons[0] = index->sons[1] = nullptr;
}
inline void pushdown(Node* index, int l, int r){
if(l==r) return;
int mid = (l+r)>>1;
if(not index->sons[0]){
index->sons[0] = new Node();
if(index->f1 == (r-l+1))
fill1(index->sons[0], l, mid);
}
if(not index->sons[1]){
index->sons[1] = new Node();
if(index->f1 == (r-l+1))
fill1(index->sons[1], mid+1, r);
}
}
inline void update(Node* index, int l, int r){
if(l==r)
return;
int mid = (l+r)>>1;
index->f1 = (index->sons[0]->f1) + (index->sons[1]->f1);
index->f2 = (index->sons[0]->f2) + (index->sons[1]->f2) + 1ll * (r-mid) * index->sons[0]->f1;
}
// fill left ks 0 to 1
void fill0to1(Node* index, int l, int r, int k){
if((r-l+1) - index->f1 == k or l == r)
return fill1(index, l, r);
pushdown(index, l, r);
int mid = (l+r)>>1;
int l0 = mid-l+1 - index->sons[0]->f1; // count 0 in left subtree
if(l0 >= k)
fill0to1(index->sons[0], l, mid, k);
else{
fill1(index->sons[0], l, mid);
fill0to1(index->sons[1], mid+1, r, k - l0);
}
update(index, l, r);
}
// fill left ks 1 to 0
void fill1to0(Node* index, int l, int r, int k){
if(index->f1 == k or l == r)
return fill0(index, l, r);
pushdown(index, l, r);
int mid = (l+r)>>1;
int l1 = index->sons[0]->f1;
if(l1 >= k)
fill1to0(index->sons[0], l, mid, k);
else{
fill0(index->sons[0], l, mid);
fill1to0(index->sons[1], mid+1, r, k - l1);
}
update(index, l, r);
}
i64 n, m, c;
int main(){
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Mem usage: %.4lf KB\n", (&Ed-&Bg) / 1024.0);
fprintf(stderr, "Mem usage: %.4lf MB\n", (&Ed-&Bg) / 1024.0 / 1024.0);
#endif
scanf("%lld%lld", &n, &m);
for(int i=1; i<=m; i++){
scanf("%lld", &c);
if(c > 0)
fill0to1(root, 1, n, c);
if(c < 0)
fill1to0(root, 1, n, -c);
printf("%lld\n", root->f2);
}
return 0;
}
P4145 上帝造题的七分钟2花神游历各国
“第一分钟,X 说,要有数列,于是便给定了一个正整数数列。
第二分钟,L 说,要能修改,于是便有了对一段数中每个数都开平方(下取整)的操作。
第三分钟,k 说,要能查询,于是便有了求一段数的和的操作。
第四分钟,彩虹喵说,要是 noip 难度,于是便有了数据范围。
第五分钟,诗人说,要有韵律,于是便有了时间限制和内存限制。
第六分钟,和雪说,要省点事,于是便有了保证运算过程中及最终结果均不超过 位有符号整数类型的表示范围的限制。
第七分钟,这道题终于造完了,然而,造题的神牛们再也不想写这道题的程序了。”
——《上帝造题的七分钟·第二部》
所以这个神圣的任务就交给你了。
P4145 上帝造题的七分钟2花神游历各国 解法
双倍经验 GSS4 Can_you_answer_these_queries_IV。
区间开方区间下取整。
这个题特别简单,首先你考虑暴力开方,并且在区间最大值为 1 的时候停止递归。
为什么这样是对的呢?因为每个数即使开最大,在十多次开方之后也会变成 1,而 ,所以就不需要继续开了。
最后开方的总复杂度为 ,可以通过。
这种数据结构叫“势能线段树”,复杂度是均摊的 后面还有。
#include <algorithm>
#include <iostream>
#include <string.h>
#include <bitset>
#include <vector>
#include <string>
#include <queue>
#include <map>
#include <set>
#include <math.h>
using std::abs;
using std::cin;
using std::copy;
using std::cout;
using std::fill;
using std::lower_bound;
using std::make_pair;
using std::map;
using std::max;
using std::min;
using std::pair;
using std::priority_queue;
using std::queue;
using std::set;
using std::sort;
using std::sqrt;
using std::string;
using std::swap;
using std::unique;
using std::upper_bound;
using std::vector;
#define mkpair make_pair
// using std::endl;
const char endl = '\n';
typedef long long i64;
typedef std::pair<int, int> pii;
typedef std::pair<i64, i64> pi64;
typedef std::vector<int> vint;
typedef std::vector<i64> vi64;
typedef std::queue<int> qint;
typedef std::queue<i64> qi64;
typedef std::priority_queue<int> pqint;
typedef std::priority_queue<i64> pqi64;
typedef long long i64;
const i64 mod = 1;
const int maxn = 2e5;
i64 n, m, sum[maxn << 2], maxx[maxn << 2];
void update(i64 index)
{
sum[index] = sum[index << 1] + sum[index << 1 | 1];
maxx[index] = max(maxx[index << 1], maxx[index << 1 | 1]);
}
void build(int index, int l, int r)
{
if (l == r)
{
cin >> sum[index];
maxx[index] = sum[index];
return;
}
int mid = (l + r) >> 1;
build(index << 1, l, mid);
build(index << 1 | 1, mid + 1, r);
update(index);
}
void modify(int index, int l, int r, int ql, int qr)
{
if (l > qr or r < ql)
return;
if (l == r)
{
sum[index] = maxx[index] = sqrt(sum[index]);
return;
}
if (maxx[index] == 1)
return;
int mid = (l + r) >> 1;
modify(index << 1, l, mid, ql, qr);
modify(index << 1 | 1, mid + 1, r, ql, qr);
update(index);
}
i64 query(int index, int l, int r, int ql, int qr)
{
if (l > qr or r < ql)
return 0;
if (ql <= l and r <= qr)
return sum[index];
int mid = (l + r) >> 1;
return query(index << 1, l, mid, ql, qr) + query(index << 1 | 1, mid + 1, r, ql, qr);
}
int t, u, v;
int main()
{
cin >> n;
build(1, 1, n);
cin >> m;
for (int i = 1; i <= m; i++)
{
cin >> t >> u >> v;
if (u > v)
swap(u, v);
if (t == 0)
modify(1, 1, n, u, v);
else
cout << query(1, 1, n, u, v) << endl;
}
return 0;
}
GSS1 Can You answer these queries I
给定长度为 的序列 。现在有 次询问操作,每次给定 ,查询 区间内的最大子权和。
区间 的最大子权和被定义为 。
,。
GSS1 Can You answer these queries I 解法
动态维护最大子段和。
对于每段区间,维护左起最大子段和,右起最大子段和,和区间中的最大子段和,然后就很好合并了。
data merge(data l, data r){
return data(
l.sum + r.sum,
max(l.ls, l.sum+r.ls),
max(l.rs+r.sum, r.rs),
max(
max(l.ts, r.ts),
l.rs+r.ls
)
);
}
然后就很简单了啊,照着题意模拟一下就秒了。
// Problem: GSS1 - Can you answer these queries I
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/SP1043
// Memory Limit: 1 MB
// Time Limit: 230000 ms
#include<stdio.h>
typedef long long i64;
const int maxn = 50007<<2;
i64 inf = 1ll << 60;
i64 max(i64 l, i64 r) { return l>r?l:r; }
i64 min(i64 l, i64 r) { return l<r?l:r; }
struct data{
i64 sum, ls, rs, ts;
data(i64 sum_=0, i64 ls_=0, i64 rs_=0, i64 ts_=0) : sum(sum_), ls(ls_), rs(rs_), ts(ts_) {}
bool operator==(const data& x) const { return sum==x.sum and ls==x.ls and rs==x.rs and rs==x.ts; }
} tree[maxn];
data merge(data l, data r){
return data(
l.sum + r.sum,
max(l.ls, l.sum+r.ls),
max(l.rs+r.sum, r.rs),
max(
max(l.ts, r.ts),
l.rs+r.ls
)
);
}
void build(int index, int l, int r){
if(l == r){
scanf("%lld", &tree[index].sum);
// printf("%d : read %d\n", index, tree[index].sum);
tree[index].ls = tree[index].rs = tree[index].ts = tree[index].sum;
// tree[index].sum;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
// printf("%d : %lld %lld %lld %lld\n", index, tree[index].sum, tree[index].ls, tree[index].rs, tree[index].ts);
}
data query(int index, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)
return tree[index];
int mid = (l+r)>>1;
if(ql > mid)
return query(index<<1|1, mid+1, r, ql, qr);
if(qr <= mid)
return query(index<<1, l, mid, ql, qr);
return merge(query(index<<1, l, mid, ql, qr),
query(index<<1|1, mid+1, r, ql, qr));
}
int n, m, u, v;
int main(){
scanf("%d", &n);
build(1, 1, n);
scanf("%d", &m);
for(int i=1;i<=m;i++){
scanf("%d%d", &u, &v);
printf("%lld\n", query(1, 1, n, u, v).ts);
}
return 0;
}
GSS3 Can you answer these queries III
单点修改,区间查询最大子段和。
GSS3 Can you answer these queries III 解法
双倍经验:P4513
先看GSS1题解。
动态带修地维护区间子段和,因为是端点修改,所以很简单。
代码和上一题很像,多个修改操作。
// Problem: GSS3 - Can you answer these queries III
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/SP1716
// Memory Limit: 1 MB
// Time Limit: 330000 ms
#include<stdio.h>
typedef long long i64;
const int maxn = 50007<<2;
i64 inf = 1ll << 60;
i64 max(i64 l, i64 r) { return l>r?l:r; }
i64 min(i64 l, i64 r) { return l<r?l:r; }
struct data{
i64 sum, ls, rs, ts;
data(i64 sum_=0, i64 ls_=0, i64 rs_=0, i64 ts_=0) : sum(sum_), ls(ls_), rs(rs_), ts(ts_) {}
bool operator==(const data& x) const { return sum==x.sum and ls==x.ls and rs==x.rs and rs==x.ts; }
} tree[maxn];
data merge(data l, data r){
return data(
l.sum + r.sum,
max(l.ls, l.sum+r.ls),
max(l.rs+r.sum, r.rs),
max(
max(l.ts, r.ts),
l.rs+r.ls
)
);
}
void build(int index, int l, int r){
if(l == r){
scanf("%lld", &tree[index].sum);
// printf("%d : read %d\n", index, tree[index].sum);
tree[index].ls = tree[index].rs = tree[index].ts = tree[index].sum;
// tree[index].sum;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
// printf("%d : %lld %lld %lld %lld\n", index, tree[index].sum, tree[index].ls, tree[index].rs, tree[index].ts);
}
data query(int index, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)
return tree[index];
int mid = (l+r)>>1;
if(ql > mid)
return query(index<<1|1, mid+1, r, ql, qr);
if(qr <= mid)
return query(index<<1, l, mid, ql, qr);
return merge(query(index<<1, l, mid, ql, qr),
query(index<<1|1, mid+1, r, ql, qr));
}
void modify(int index, int l, int r, int pos, int v){
if(l == r and l == pos){
tree[index].ls = tree[index].rs = tree[index].ts = tree[index].sum = v;
return;
}
if(l > pos or r < pos)
return;
int mid = (l+r)>>1;
modify(index<<1, l, mid, pos, v);
modify(index<<1|1, mid+1, r, pos, v);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
int n, m, t, u, v, w;
int main(){
scanf("%d", &n);
build(1, 1, n);
scanf("%d", &m);
for(int i=1;i<=m;i++){
scanf("%d", &t);
if(t == 0)
scanf("%d%d", &u, &v),
modify(1, 1, n, u, v);
else
scanf("%d%d", &u, &v),
printf("%d\n", query(1, 1, n, u, v).ts);
// scanf("%d%d", &u, &v);
// printf("%lld\n", query(1, 1, n, u, v).ts);
}
return 0;
}
abc322f Vacation Query
给你一个长度为 的字符串 ,由 0 和 1 组成。让 表示 的第 个字符。
按照给出的顺序处理个查询。
每个查询由三个整数组成的元组表示,其中表示查询的类型。
- 当 时:对于每个整数,如果是 “1”,则将改为 “0”;如果是 “0”,则将改为 “1”。
- 当 :设是提取的第个到第个字符后得到的字符串。打印 中连续
1的最大数目。
abc322f Vacation Query 解法
这道题题意简单,说白了就是区间翻转,查询区间最长1。
既然可以用线段树维护,那么这个区间就一定有可以用线段树维护的一些性质。
那么一个区间应该记录如下信息:
- 从左侧起的最长0和1(记0是为了翻转)
- 从右侧起的最长0和1
- 整段的最长0和1
struct seq
{
int llong, rlong, along;
seq(int llong_ = 0, int rlong_ = 0, int along_ = 0) : llong(llong_), rlong(rlong_), along(along_) {}
};
这样我们在合并区间的时候就可以变为如下:
seq merge(seq a, seq b, int llen, int rlen)
{
seq res;
res.llong = a.llong + (a.llong == llen) * b.llong, res.rlong = b.rlong + (b.rlong == rlen) * a.rlong;
res.along = max(max(max(res.llong, res.rlong), a.rlong + b.llong), max(a.along, b.along));
return res;
}
这样答案是不重不漏的。为了维护区间 01 翻转,所以要对于 0 和 1同时记录区间信息。
struct treedata
{
seq dat[2];
};
treedata initial(int x)
{
treedata res;
res.dat[1].llong = x, res.dat[1].rlong = x, res.dat[1].along = x, res.dat[0].llong = x ^ 1, res.dat[0].rlong = x ^ 1, res.dat[0].along = x ^ 1;
return res;
}
treedata merge(treedata a, treedata b, int llen, int rlen)
{
treedata res;
res.dat[0] = merge(a.dat[0], b.dat[0], llen, rlen), res.dat[1] = merge(a.dat[1], b.dat[1], llen, rlen);
return res;
}
然后就是主体线段树,记得精细实现。
struct segtree
{
int l, r;
treedata data;
int rev;
segtree(int l_ = 0, int r_ = 0, treedata data_ = treedata(), int rev_ = 0) : l(l_), r(r_), data(data_), rev(rev_) {}
} tree[maxn];
void build(int index, int l, int r, int *val)
{
tree[index].l = l, tree[index].r = r;
if (l == r)
return void(tree[index].data = initial(val[l]));
int mid = (l + r) >> 1;
build(index << 1, l, mid, val), build(index << 1 | 1, mid + 1, r, val);
return void(tree[index].data = merge(tree[index << 1].data, tree[index << 1 | 1].data, (mid - tree[index].l + 1), (tree[index].r - (mid + 1) + 1)));
}
void setlazy(int index) { swap(tree[index].data.dat[0], tree[index].data.dat[1]), tree[index].rev ^= 1; }
void pushlazy(int index)
{
if (tree[index].rev)
setlazy(index << 1), setlazy(index << 1 | 1), tree[index].rev = 0;
}
void reverse(int index, int l, int r)
{
pushlazy(index);
if (l <= tree[index].l and tree[index].r <= r)
return setlazy(index);
if (l > tree[index].r or r < tree[index].l)
return;
int mid = (tree[index].l + tree[index].r) >> 1;
reverse(index << 1, l, r), reverse(index << 1 | 1, l, r);
tree[index].data = merge(tree[index << 1].data, tree[index << 1 | 1].data, (mid - tree[index].l + 1), (tree[index].r - (mid + 1) + 1));
}
seq query(int index, int l, int r)
{
pushlazy(index);
if (l <= tree[index].l and tree[index].r <= r)
return tree[index].data.dat[1];
int mid = (tree[index].l + tree[index].r) >> 1;
if (l >= mid + 1)
return query(index << 1 | 1, l, r);
if (r <= mid)
return query(index << 1, l, r);
return merge(query(index << 1, l, r), query(index << 1 | 1, l, r), mid - tree[index].l + 1, tree[index].r - (mid + 1) + 1);
}
主程序很简单。
int n, m, li[maxn];
int t, u, v;
char ch;
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
do
ch = getchar();
while (ch != '0' && ch != '1');
li[i] = ch ^ 48;
}
build(1, 1, n, li);
for (int i = 1; i <= m; i++)
{
cin >> t >> u >> v;
if (t == 1)
reverse(1, u, v);
if (t == 2)
cout << query(1, u, v).along << endl;
}
return 0;
}
CF1862F Magic Will Save the World
Vika 需要打败 只怪物,第 只怪物的血量为 。
Vika 可以念 水系咒语 或 火系咒语 来给怪物造成伤害,但第 只怪物被击败当且仅当它受到了 的水系咒语伤害或 的火系咒语伤害。Vika 每秒可以念无限条咒语。
Vika 每秒会获得 个单位的 水系能量 和 个单位的 火系能量, 个单位的能量可以转化成伤害为 的对应系咒语。Vika 初始拥有的水系、火系能量均为 个单位。
问 Vika 至少需要多少秒才能击败全部怪物。
CF1862F Magic Will Save the World 解法
收集魔法到最后再用肯定没问题。
并且要保证每种怪物只收到一种魔法的攻击。
所以考虑用背包+bitset优化,枚举所有可能的怪物的强度之和,用 A 魔法解决,剩下的用 B。
const i64 mod = 1;
const i64 maxn = 1.2e6;
std::bitset<maxn> b;
int n, sum, w, f, ti = 2e9;
std::vector<int> mons;
void solve()
{
ti = 2e9;
cin >> w >> f;
b = 1;
n = sum = 0;
cin >> n;
in_vec(mons, n);
info(w, f, n);
array(mons);
for (int i = 0; i < n; i++)
sum += mons[i],
b = b | (b << mons[i]);
for (int x = 0; x < maxn; x++)
if (b[x])
{
info(x, sum - x, (x + w - 1) / w, (sum - x + f - 1) / f, max((x + w - 1) / w, (sum - x + f - 1) / f));
ti = min(ti, max((x + w - 1) / w, (sum - x + f - 1) / f));
}
// printf("%d\n", ti);
cout << ti << endl;
}
// g++ -o run -std=c++14 -D debug_rickyxrc -Wall -Wextra -Wshadow -fsanitize=undefined
CF1149C Tree Generator
(建议看原题的英文)
个点,个询问。
给你一棵树的括号序列,输出它的直径。
有次询问,每次询问表示交换两个括号,输出交换两个括号后的直径(保证每次操作后都为一棵树)
输出共行。
CF1149C Tree Generator 解法
树的直径:树上最远两点的距离。
我们发现这样一个性质:树上两点间的距离等于两点的括号序列最简化后的长度。
发现有修改操作,于是考虑上线段树。
每个节点需要维护左起/右起最长/最短未匹配括号。
为了让最简化后的长度最长,我们考虑维护左起/右起最长/最短未匹配括号最大/最小/最大 delta。
详见 merge 函数,剩下的就是 GSS3 的操作。
// Problem: C. Tree Generator™
// Contest: Codeforces - Codeforces Round 556 (Div. 1)
// URL: https://codeforces.com/problemset/problem/1149/C
// Memory Limit: 256 MB
// Time Limit: 2000 ms
#include<stdio.h>
const int maxn = 6e5;
int min(int a, int b) { return a<b?a:b; }
int max(int a, int b) { return a>b?a:b; }
char lsum[maxn];
struct data {
int sum, // answer
lsmax, lsmin, rsmax, rsmin,
ldmax, rdmax,
dlmax, ans;
data(int sum_=0,
int lsmax_=0, int lsmin_=0, int rsmax_=0, int rsmin_=0,
int ldmax_=0, int rdmax_=0,
int dlmax_=0, int ans_=0) :
sum(sum_), lsmax(lsmax_), lsmin(lsmin_), rsmax(rsmax_), rsmin(rsmin_),
ldmax(ldmax_), rdmax(rdmax_),
dlmax(dlmax_), ans(ans_) {}
} tree[maxn];
void merge(int index) {
tree[index].sum = tree[index<<1].sum + tree[index<<1|1].sum;
tree[index].lsmax = max(tree[index<<1].lsmax, tree[index<<1].sum + tree[index<<1|1].lsmax);
tree[index].rsmax = max(tree[index<<1|1].rsmax, tree[index<<1|1].sum + tree[index<<1].rsmax);
tree[index].lsmin = min(tree[index<<1].lsmin, tree[index<<1].sum + tree[index<<1|1].lsmin);
tree[index].rsmin = min(tree[index<<1|1].rsmin, tree[index<<1|1].sum + tree[index<<1].rsmin);
tree[index].ldmax = max(max(tree[index<<1].ldmax, tree[index<<1|1].ldmax - tree[index<<1].sum), tree[index<<1].dlmax + tree[index<<1|1].lsmax);
tree[index].rdmax = max(max(tree[index<<1|1].rdmax,tree[index<<1|1].sum + tree[index<<1].rdmax),tree[index<<1|1].dlmax - tree[index<<1].rsmin );
tree[index].dlmax = max(tree[index<<1].dlmax+tree[index<<1|1].sum, tree[index<<1|1].dlmax-tree[index<<1].sum);
tree[index].ans = max(max(tree[index<<1].ans, tree[index<<1|1].ans),
max(tree[index<<1|1].ldmax - tree[index<<1].rsmin, tree[index<<1].rdmax + tree[index<<1|1].lsmax));
}
data initial(char s) {
if(s == '(')
return data(1, 1, 0, 1, 0, 1, 1, 1, 1); // (
return data(-1, 0, -1, 0, -1, 1, 1, 1, 1); // )
}
char ch;
void build(int index, int l, int r) {
if(l == r){
do
ch = getchar();
while(ch!='(' and ch!=')');
lsum[l] = ch;
tree[index] = initial(ch);
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
merge(index);
}
void modify(int index, int l, int r, int pos, char v) {
if(l == r and l == pos) {
tree[index] = initial(v);
return;
}
if(l > pos or r < pos)
return;
int mid = (l+r)>>1;
modify(index<<1, l, mid, pos, v);
modify(index<<1|1, mid+1, r, pos, v);
merge(index);
}
int n, m, u, v;
int main() {
scanf("%d%d",&n,&m);
n = 2*n-2;
build(1, 1, n);
printf("%d\n", tree[1].ans);
for(int i=1;i<=m;i++){
scanf("%d%d", &u, &v);
modify(1, 1, n, u, lsum[v]);
modify(1, 1, n, v, lsum[u]);
lsum[u] ^= lsum[v] ^= lsum[u] ^= lsum[v];
printf("%d\n", tree[1].ans);
}
return 0;
}
CF438D The Child and Sequence
有一个长度为 的数列 和 次操作,操作内容如下:
- 格式为
1 l r,表示求 的值并输出。 - 格式为
2 l r x,表示对区间 内每个数取模,模数为 。 - 格式为
3 k x,表示将 修改为 。
CF438D The Child and Sequence 解法
使用势能线段树,发现区间取模后每个数都会小于等于 。
所以就暴力修改,区间最大值要是小于 取模就是没有意义的,直接返回即可。
// Problem: D. The Child and Sequence
// Contest: Codeforces - Codeforces Round 250 (Div. 1)
// URL: https://codeforces.com/problemset/problem/438/D
// Memory Limit: 256 MB
// Time Limit: 4000 ms
#include<stdio.h>
typedef long long i64;
bool memend;
const int maxn = 4.2e5;
int n, m;
struct data{
i64 maxv, sum;
} tree[maxn];
i64 max(i64 a,i64 b) { return a>b?a:b; }
void update(int index) {
tree[index].sum = tree[index<<1].sum + tree[index<<1|1].sum;
tree[index].maxv = max(tree[index<<1].maxv, tree[index<<1|1].maxv);
}
void build(int index, int l, int r){
if(l == r) {
scanf("%lld", &tree[index].sum);
// printf("read %d, %d\n", l, tree[index].sum);
tree[index].maxv = tree[index].sum;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
update(index);
}
i64 query(int index, int l, int r, int ql, int qr){
if(ql <= l and r <= qr)
return tree[index].sum;
if(l > qr or r < ql)
return 0;
int mid = (l+r)>>1;
return query(index<<1, l, mid, ql, qr) +
query(index<<1|1, mid+1, r, ql, qr);
}
void modify(int index, int l, int r, int pos, int v){
if(pos <= l and r <= pos){
// printf("modify %d <- %d\n", l, v);
return void(tree[index].sum = tree[index].maxv = v);
}
if(l > pos or r < pos)
return;
int mid = (l+r)>>1;
modify(index<<1, l, mid, pos, v);
modify(index<<1|1, mid+1, r, pos, v);
update(index);
}
void smod(int index, int l, int r, int ql, int qr, int mod){
if(ql <= l and r <= qr and l == r)
return void(tree[index].maxv = (tree[index].sum %= mod));
if(l > qr or r < ql or tree[index].maxv < mod)
return;
int mid = (l+r)>>1;
smod(index<<1, l, mid, ql, qr, mod);
smod(index<<1|1, mid+1, r, ql, qr, mod);
update(index);
}
int t, u, v, w;
bool membegin;
int main(){
#ifdef debug_rickyxrc
fprintf(stderr, "Memory usage : %.4lf KB\n", (&memend-&membegin) / 1024.0);
fprintf(stderr, "Memory usage : %.4lf MB\n", (&memend-&membegin) / 1024.0 / 1024.0);
#endif
scanf("%d%d", &n, &m);
build(1, 1, n);
for(int i=1;i<=m;i++){
scanf("%d", &t);
if(t == 1)
scanf("%d%d", &u, &v),
printf("%lld\n", query(1, 1, n, u, v));
else if(t==2)
scanf("%d%d%d", &u, &v, &w),
smod(1, 1, n, u, v, w);
// else
// return 0;
else if(t==3)
scanf("%d%d", &u, &w),
modify(1, 1, n, u, w);
}
return 0;
}
P2886 Cow Relays G
给出一张无向连通图,求 到 经过 条边的最短路。
P2886 Cow Relays G 解法
矩阵快速幂的板子,需要使用广义矩阵乘法。
matrix operator*(matrix a, matrix b)
{
matrix res;
for (int k = 0; k < maxn; k++)
for (int i = 0; i < maxn; i++)
for (int j = 0; j < maxn; j++)
res[i][j] = min(res[i][j], a[i][k] + b[k][j]);
return res;
}
和 floyd 的过程比对一下就能理解。
// Problem: P2886 [USACO07NOV] Cow Relays G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2886
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include <stdio.h>
#include <string.h>
#define maxn 201
typedef long long i64;
i64 min(i64 a, i64 b) { return a<b?a:b; }
struct matrix
{
i64 data[maxn][maxn];
matrix() { memset(data, 0x3f, sizeof data); }
i64 *operator[](i64 index) { return data[index]; }
};
matrix operator*(matrix a, matrix b)
{
matrix res;
for (int k = 0; k < maxn; k++)
for (int i = 0; i < maxn; i++)
for (int j = 0; j < maxn; j++)
res[i][j] = min(res[i][j], a[i][k] + b[k][j]);
return res;
}
matrix pow(matrix x, i64 p)
{
matrix res = x;
p--;
while (p)
{
if (p & 1)
res = res * x;
x = x * x;
p >>= 1;
}
return res;
}
matrix c;
int n, m, s, t, a, b, u, v, w, res;
int val[2000], cnt;
int main()
{
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i=1;i<=m;i++){
scanf("%d%d%d", &w, &u, &v);
if(!val[u]) val[u] = ++cnt;
if(!val[v]) val[v] = ++cnt;
u = val[u], v = val[v];
c[u][v] = c[v][u] = min(c[u][v], w);
}
c = pow(c, n);
printf("%lld\n", c[val[s]][val[t]]);
return 0;
}
CF446C DZY Loves Fibonacci Numbers
- 在本题中,我们用 来表示第 个斐波那契数()。
- 维护一个序列 ,长度为 ,有 次操作:
1 l r:对于 ,将 加上 。2 l r:求 。
- ,。
CF446C DZY Loves Fibonacci Numbers 解法
区间加 fib 一看就不是很可做,有两种做法。
我使用的是少见的那种。看起来我不喜欢常规做法
已知:
发现它是两个等比数列的差,恰巧这题又有 ,不用扩域!所以就可以变成如下一个问题:
- 区间加一个等比数列
- 查询区间求和
因为等比数列的公比是一样的,所以首项可加。
在更新的时候需要等比数列求和公式,并预处理幂来防止复杂度到达 。
因为 ,代码里面就偷懒了点没分开。
// Problem: DZY Loves Fibonacci Numbers
// Contest: Luogu
// URL: https://codeforces.com/problemset/problem/446/C
// Memory Limit: 250 MB
// Time Limit: 4000 ms
#include<stdio.h>
const int maxn = 6.1e5;
const int mod = 1000000009;
const int sqrt5 = 616991993; // = sqrt(5)
const int sqrt5inv = 723398404; // = 1/sqrt(5)
const int inv2 = 500000005; // = (mod+1)/2
const int q1 = 308495997; // = (sqrt5+1)/2 | 1/(q1-1) = q1
const int q2 = 691504013; // = (1-sqrt5)/2 | 1/(q2-1) = q2
int n, m, q;
int li[maxn];
inline int modadd(int x, int y) { return (x+y>=mod)?(x+y-mod):(x+y); }
inline int modmul(int x, int y) { return 1ll * x * y % mod; }
int pow(int x, int p){
int res = 1;
while(p) {
if(p&1)
res = 1ll * res * x % mod;
x = 1ll * x * x % mod;
p>>=1;
}
return res;
}
// special : 1/(1-q) = q
template <const int q>
struct sumsegtree{
int data[maxn<<2], lazy[maxn<<2], pows[maxn];
void init(int n){
pows[0] = 1;
for(int i=1;i<=n;i++)
pows[i] = modmul(pows[i-1], q);
}
void setlazy(int index, int l, int r, int v){
data[index] = modadd(data[index], modmul(v, modmul(modadd(pows[r-l+1], mod-1), q/*1/(1-q)*/)));
lazy[index] = modadd(lazy[index], v);
}
void push(int index, int l, int r){
if(!lazy[index]) return;
int mid = (l+r)>>1;
setlazy(index<<1 , l, mid, lazy[index]);
setlazy(index<<1|1, mid+1, r, modmul(lazy[index], pows[mid-l+1]));
lazy[index]=0;
}
int querysum(int index, int l, int r, int ql, int qr){
push(index, l, r);
if(ql <= l and r <= qr) return data[index];
if(l > qr or r < ql) return 0;
int mid = (l+r)>>1;
return modadd(querysum(index<<1, l, mid, ql, qr),
querysum(index<<1|1, mid+1, r, ql, qr));
}
void add(int index, int l, int r, int ql, int qr){
push(index, l, r);
if(ql <= l and r <= qr) {
setlazy(index, l, r, pows[l-ql+1]);
return;
}
if(l > qr or r < ql) return;
int mid = (l+r)>>1;
add(index<<1, l, mid, ql, qr), add(index<<1|1, mid+1, r, ql, qr);
data[index] = modadd(data[index<<1], data[index<<1|1]);
}
};
sumsegtree<q1> seg1;
sumsegtree<q2> seg2;
int sums[maxn];
int u, v, w;
int main(){
scanf("%d%d", &n, &m);
seg1.init(n);
seg2.init(n);
for(int i=1; i<=n; i++)
scanf("%d", sums+i);
for(int i=1; i<=n; i++)
sums[i] = modadd(sums[i], sums[i-1]);
for(int i=1; i<=m; i++){
scanf("%d%d%d", &u, &v, &w);
if(u == 2){
printf("%d\n", modadd(modadd(sums[w], mod-sums[v-1]),
modmul(sqrt5inv,
modadd(
seg1.querysum(1, 1, n, v, w),
mod-seg2.querysum(1, 1, n, v, w)
))));
}
else{
seg1.add(1, 1, n, v, w);
seg2.add(1, 1, n, v, w);
}
}
return 0;
}
P2597 灾难
阿米巴是小强的好朋友。
阿米巴和小强在草原上捉蚂蚱。小强突然想,如果蚂蚱被他们捉灭绝了,那么吃蚂蚱的小鸟就会饿死,而捕食小鸟的猛禽也会跟着灭绝,从而引发一系列的生态灾难。
学过生物的阿米巴告诉小强,草原是一个极其稳定的生态系统。如果蚂蚱灭绝了,小鸟照样可以吃别的虫子,所以一个物种的灭绝并不一定会引发重大的灾难。
我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系:
- 一个食物网有 个点,代表 种生物,生物从 到 编号。
- 如果生物 可以吃生物 ,那么从 向 连一个有向边。
- 这个图没有环。
- 图中有一些点没有连出边,这些点代表的生物都是生产者,可以通过光合作用来生存。
- 而有连出边的点代表的都是消费者,它们必须通过吃其他生物来生存。
- 如果某个消费者的所有食物都灭绝了,它会跟着灭绝。
我们定义一个生物在食物网中的“灾难值”为,如果它突然灭绝,那么会跟着一起灭绝的生物的种数。
举个例子:在一个草场上,生物之间的关系如下
如果小强和阿米巴把草原上所有的羊都给吓死了,那么狼会因为没有食物而灭绝,而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以,羊的灾难值是 。但是,如果草突然灭绝,那么整个草原上的 种生物都无法幸免,所以,草的灾难值是 。
给定一个食物网,你要求出每个生物的灾难值。
P2597 灾难 解法
考场上做出来了!我说的不是ZJOI2012
发现那个关系十分难处理,那先考虑弱化情形。
如果每个点只有至多一个依赖的点,那这个 DAG 就构成一个森林,灾难值可以轻易地计算(子树和)。
模拟几下样例发现,若当前节点的所有依赖均在一棵树中,那么当前节点的存活条件和当前节点的所有依赖的最近公共祖先相同(充要条件)。
但是原图是一棵森林啊,不好做,所以考虑包含 这个点,这样的话就是一棵树了。
按照拓扑序建出这棵树即可,因为要动态加点,所以考虑倍增 LCA。
#include<stdio.h>
#include<bitset>
#include<vector>
#include<queue>
using namespace std;
bool mend;
const int maxn = 65537;
const int maxh = 17;
int fas[maxn][maxh], size[maxn], depth[maxn];
int n, u;
vector<int> edge[maxn];
vector<int> reqs[maxn], graph[maxn];
int ins[maxn];
queue<int> q;
bool mbegin;
#ifdef debug_rickyxrc
void assert_val(bool val, char* failed){
if(not val)
printf("%s FAILED.\n", failed);
}
#else
#define assert_val
#endif
int lca(int u, int v){
if(depth[v] > depth[u])
return lca(v, u);
assert_val(depth[u] >= depth[v], "lca::depth_first_check");
for(int i=maxh-1;i>=0;i--)
if(depth[fas[u][i]] >= depth[v])
u = fas[u][i];
assert_val(depth[u] == depth[v], "lca::depth_second_check");
if(u == v)
return u;
for(int i=maxh-1;i>=0;i--)
if(fas[u][i] != fas[v][i])
u = fas[u][i], v = fas[v][i],
assert_val(depth[u] == depth[v], "lca::depth_jump_check");
u = fas[u][0], v = fas[v][0];
assert_val(u == v, "lca::depth_third_check");
return u;
}
int lcasum(const vector<int>& v){
if(v.size() == 1)
return 0;
int f = v[0];
for(int i=1;i<v.size()-1;i++)
f = lca(f, v[i]);
return f;
}
void initfa(int index, int fa){
edge[index].push_back(fa);
edge[fa].push_back(index);
depth[index] = depth[fa]+1;
fas[index][0] = fa;
for(int i=1;i<maxh;i++)
fas[index][i] = fas[fas[index][i-1]][i-1];
}
void initsize(int index, int fa){
size[index]=1;
for(auto u: edge[index])
if(u!=fa){
initsize(u, index);
size[index]+=size[u];
}
}
int main(){
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Memory usage: %.4lf KB\n", (&mend-&mbegin) / 1024.0);
fprintf(stderr, "Memory usage: %.4lf MB\n", (&mend-&mbegin) / 1024.0 / 1024.0);
#endif
scanf("%d", &n);
for(int i=1;i<=n;i++)
do{
scanf("%d", &u);
reqs[i].push_back(u);
graph[u].push_back(i);
ins[i]++;
}while(u);
q.push(0);
while(not q.empty()) {
int u = q.front();q.pop();
if(u!=0) {
int ans = lcasum(reqs[u]);
initfa(u, ans);
}
for(auto v:graph[u])
if(--ins[v] == 0)
q.push(v);
}
initsize(0, -1);
for(int i=1;i<=n;i++)
printf("%d\n", size[i]-1);
return 0;
}
P2601 对称的正方形
Orez 很喜欢搜集一些神秘的数据,并经常把它们排成一个矩阵进行研究。最近,Orez 又得到了一些数据,并已经把它们排成了一个 行 列的矩阵。通过观察,Orez 发现这些数据蕴涵了一个奇特的数,就是矩阵中上下对称且左右对称的正方形子矩阵的个数。Orez 自然很想知道这个数是多少,可是矩阵太大,无法去数。只能请你编个程序来计算出这个数。
P2601 对称的正方形 解法
二维 hash 的板子。
考虑矩阵的 hash 为 为 hash 贡献 。
这样的话可以求出子矩阵的 hash 值。
然后发现对称矩阵的存在性和大小有单调性(固定中心时),最后二分一下就好。
不用分奇偶性讨论,在中间插入相同的值就行了,就像下面这样:
1 1
1 1
---
1 0 1
0 0 0
1 0 1
双 hash 没过去,中间很长的代码都白写了。
#include<stdio.h>
#include<ctype.h>
inline int min(int a, int b) { return a<b?a:b; }
inline int max(int a, int b) { return a>b?a:b; }
template <const int mod> struct modint;
template <const int mod> modint<mod> pow(modint<mod> x, int p){
modint<mod> res(1);
while(p){
if(p&1)
res*=x;
x*=x;
p>>=1;
}
return res;
}
template <const int mod> struct modint{
int x;
modint(int v=0){
#ifdef debug_rickyxrc
if(v<0 or v>=mod)
printf("modint::modint<%d>(%d:int) : Error : %d overflow.\n", mod, v, v);
#endif
this->x = v;
}
modint<mod> inv() const { return pow(*this, mod-2); }
};
template <const int mod> bool operator==(modint<mod> a, modint<mod> b) { return a.x==b.x; }
template <const int mod> const modint<mod> operator+(modint<mod> a, modint<mod> b) { return modint<mod>(a.x+b.x>=mod?a.x+b.x-mod:a.x+b.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a) { return a.x==0?0:modint<mod>(mod-a.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a, modint<mod> b) { return a + (-b); }
template <const int mod> const modint<mod> operator*(modint<mod> a, modint<mod> b) { return modint<mod>(1ll * a.x * b.x % mod); }
template <const int mod> const modint<mod> operator/(modint<mod> a, modint<mod> b) { return a * b.inv(); }
template <const int mod> const modint<mod> operator+=(modint<mod>& a, modint<mod> b) { return a = a+b; }
template <const int mod> const modint<mod> operator-=(modint<mod>& a, modint<mod> b) { return a = a-b; }
template <const int mod> const modint<mod> operator*=(modint<mod>& a, modint<mod> b) { return a = a*b; }
template <const int mod> const modint<mod> operator/=(modint<mod>& a, modint<mod> b) { return a = a/b; }
template <const int mod1, const int mod2> struct double_modint {
modint<mod1> x1;
modint<mod2> x2;
double_modint(int v1=0) : x1(v1), x2(v1) {}
double_modint(modint<mod1> v1, modint<mod2> v2) : x1(v1), x2(v2) {}
double_modint<mod1, mod2> inv() const{
return double_modint<mod1, mod2>(x1.inv(), x2.inv());
}
};
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator+ (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1+b.x1, a.x2+b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator- (double_modint<mod1, mod2> a) { return double_modint<mod1, mod2>(-a.x1, -a.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator- (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1-b.x1, a.x2-b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator* (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1*b.x1, a.x2*b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator/ (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1/b.x1, a.x2/b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator+= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a+b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator-= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a-b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator*= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a*b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator/= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a/b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> pow(double_modint<mod1, mod2> x, int p) { return double_modint<mod1, mod2>(pow<mod1> (x.x1, p), pow<mod2> (x.x2, p)); }
template <const int mod1, const int mod2> bool operator==(double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return (a.x1==b.x1) and (a.x2==b.x2);}
const int mod1 = 998244353, mod2 = 998244853;
using hashval = modint<mod1>;
#ifndef debug_rickyxrc
const hashval p1 = 387, p2 = 961;
#else
const hashval p1 = 7, p2 = 11;
#endif
bool edmem;
const int maxn = 2014;
hashval hashn[maxn][maxn], hashri[maxn][maxn], hashrj[maxn][maxn];
int n, m;
int mp[maxn][maxn];
hashval powp1[maxn], powp2[maxn];
bool bgmem;
struct point {
int i, j;
point(int i_=0, int j_=0) : i(i_), j(j_) {}
point mirror_i() { return point(n-i, j); }
point mirror_j() { return point(i, m-j); }
};
inline point operator+(point a, point b) { return point(a.i+b.i, a.j+b.j); }
inline point operator-(point a) { return point(-a.i, -a.j); }
inline point operator-(point a, point b) { return a + (-b); }
template <class T> inline T getv(T vals[][maxn], point p1) { return vals[p1.i][p1.j]; }
template <class T> inline T directsum(T vals[][maxn], point p1, point p2){
T res = getv(vals, p2);
if(p1.i) res -= getv(vals, point(p1.i-1, p2.j));
if(p1.j) res -= getv(vals, point(p2.i, p1.j-1));
if(p1.i and p1.j) res += getv(vals, p1 - point(1, 1));
return res;
}
template <class T> inline void getsum(T vals[][maxn]){
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
vals[i][j] += vals[i-1][j] + vals[i][j-1] - vals[i-1][j-1];
}
inline hashval directhash(hashval vals[][maxn], point a, point b) {
return directsum(vals, a, b) * powp1[a.i] * powp2[b.j];
}
inline hashval commonhash(point a, point b) { return directhash(hashn, a, b); }
inline hashval revihash(point a, point b) {
a = a.mirror_i(), b = b.mirror_i();
return directhash(hashri, point(b.i, a.j), point(a.i, b.j));
}
inline hashval revjhash(point a, point b) {
a = a.mirror_j(), b = b.mirror_j();
return directhash(hashrj, point(a.i, b.j), point(b.i, a.j));
}
inline bool equal(point a, point b) {
hashval val1 = commonhash(a, b),
val2 = revihash(a, b),
val3 = revjhash(a, b);
return val1 == val2 and val2 == val3;
}
inline int readi()
{
char c=getchar();int x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;return x;
}
int main() {
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Memory usage : %.4lf KB\n", (&edmem-&bgmem) / 1024.0);
fprintf(stderr, "Memory usage : %.4lf MB\n", (&edmem-&bgmem) / 1024.0 / 1024.0);
#endif
scanf("%d%d", &n, &m);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
mp[i<<1|1][j<<1|1] = readi();
n = 2*n, m = 2*m;
powp1[0] = powp2[0] = hashval(1);
int e = max(n, m);
const hashval p1i = p1.inv(), p2i = p2.inv();
for(int i=1; i<=e;i++)
powp1[i] = powp1[i-1] * p1i,
powp2[i] = powp2[i-1] * p2i;
hashval x = 1, y = 1;
for(int i=1;i<=n;i++, x*=p1) {
y = 1;
for(int j=1;j<=m;j++, y*=p2)
hashn [i][j] = hashval(getv(mp, point(i, j))) * x * y,
hashri[i][j] = hashval(getv(mp, point(i, j).mirror_i())) * x * y,
hashrj[i][j] = hashval(getv(mp, point(i, j).mirror_j())) * x * y;
}
getsum(hashn);
getsum(hashri);
getsum(hashrj);
long long ans=0;
for(int i=1;i<n;i++)
for(int j=1;j<m;j++) {
if(i%2 xor j%2) continue;
int r = min(min(i, n-i), min(m-j, j)), l = 1;
while(r-l>1) {
int mid = (l+r)>>1;
if(equal(point(i-mid, j-mid), point(i+mid, j+mid)))
l = mid;
else
r = mid-1;
}
for(int mid=r;mid>=l;mid--)
if(equal(point(i-mid, j-mid), point(i+mid, j+mid))) {
ans += mid/2;
break;
}
}
printf("%lld\n", ans+n*1ll/2*m*1ll/2);
return 0;
}
P2592 生日聚会
P2592 生日聚会 解法
定义 表示放了i个男生,j个女生,所有后缀中,男生减女生的差最大为k,女生减男生的差最大为h的方案数(这谁想得到啊)。
转移十分简单。
#include<stdio.h>
const int maxn = 157;
const int maxk = 27;
bool edmem;
const int mod = 12345678;
int f[maxn][maxn][maxk][maxk];
int n, m, d;
bool bgmem;
int max(int a, int b) { return a>b?a:b; }
int main() {
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Memory usage : %.4lf KB\n", (&edmem-&bgmem) / 1024.0);
fprintf(stderr, "Memory usage : %.4lf MB\n", (&edmem-&bgmem) / 1024.0 / 1024.0);
#endif
scanf("%d%d%d", &n, &m, &d);
f[0][0][0][0] = 1;
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++)
for(int k=0;k<=d;k++)
for(int h=0;h<=d;h++)
(f[i+1][j][k+1][max(h-1, 0)] += f[i][j][k][h]) %= mod,
(f[i][j+1][max(k-1, 0)][h+1] += f[i][j][k][h]) %= mod;
int ans = 0;
for(int i=0;i<=d;i++)
for(int j=0;j<=d;j++)
(ans+=f[n][m][i][j])%=mod;
printf("%d\n", ans);
return 0;
}
P4514 上帝造题的七分钟
“第一分钟,X 说,要有矩阵,于是便有了一个里面写满了 的 矩阵。
第二分钟,L 说,要能修改,于是便有了将左上角为 ,右下角为 的一个矩形区域内的全部数字加上一个值的操作。
第三分钟,k 说,要能查询,于是便有了求给定矩形区域内的全部数字和的操作。
第四分钟,彩虹喵说,要基于二叉树的数据结构,于是便有了数据范围。
第五分钟,和雪说,要有耐心,于是便有了时间限制。
第六分钟,吃钢琴男说,要省点事,于是便有了保证运算过程中及最终结果均不超过 位有符号整数类型的表示范围的限制。
第七分钟,这道题终于造完了,然而,造题的神牛们再也不想写这道题的程序了。”。
——《上帝造裸题的七分钟》。
所以这个神圣的任务就交给你了。
P4514 上帝造题的七分钟 解法
我们需要矩阵加,求矩阵的和。
使用二维树状数组,在差分数组上单点修改,在二阶前缀和数组上单点查询。
定义 为原数列的差分数组,我们得到如下公式:
所以用四个树状数组分别维护四个值就好了。
// Problem: P4514 上帝造题的七分钟
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4514
// Memory Limit: 128 MB
// Time Limit: 2000 ms
#include<stdio.h>
const int maxn = 2507;
int lowbit(int x) { return x&(-x); }
int sum[maxn][maxn], isum[maxn][maxn], jsum[maxn][maxn], ijsum[maxn][maxn];
void addt(int li[][maxn], int x, int y, int p) {
for(int x1=x; x1<maxn; x1+=lowbit(x1))
for(int yy=y; yy<maxn; yy+=lowbit(yy))
li[x1][yy] += p;
}
int query(int li[][maxn], int x, int y){
int res=0;
for(int x1=x;x1;x1-=lowbit(x1))
for(int yy=y;yy;yy-=lowbit(yy))
res += li[x1][yy];
return res;
}
void singleadd(int i, int j, int v) {
addt(sum , i, j, v);
addt(jsum , i, j, v * 1ll * j);
addt(isum , i, j, v * 1ll * i);
addt(ijsum, i, j, v * 1ll * i * j);
}
int singlequery(int i, int j) {
return (i+1ll) * (j+1ll) * query(sum, i, j)
- (i+1ll) * query(jsum, i, j)
- (j+1ll) * query(isum, i, j)
+ 1ll * query(ijsum, i, j);
}
char op;
int n, m, w, h, ldi, ldj, rui, ruj, v;
int main(){
getchar();
scanf("%d%d", &n, &m);
while(true) {
do {
op = getchar();
if(op == EOF)
return 0;
} while(op!='L' and op!='k');
if(op=='L') {
scanf("%d%d%d%d%d", &ldi, &ldj, &rui, &ruj, &v), rui++, ruj++,
singleadd(ldi, ldj, v);
singleadd(ldi, ruj, -v);
singleadd(rui, ldj, -v);
singleadd(rui, ruj, v);
}
else
scanf("%d%d%d%d", &ldi, &ldj, &rui, &ruj), ldi--, ldj--,
printf("%d\n",
singlequery(ldi, ldj) + singlequery(rui, ruj)
- singlequery(ldi, ruj) - singlequery(rui, ldj)
);
}
return 0;
}
要是范围更大,但是支持离线的话,可以考虑离线下来做,这样空间就是一维的。
CF558E A Simple Task
双倍经验:P2787 语文1(chin1)- 理理思维
题目大意: 给定一个长度不超过10^5的字符串(小写英文字母),和不超过50000个操作。
每个操作 L R K 表示给区间[L,R]的字符串排序,K=1为升序,K=0为降序。
最后输出最终的字符串。
CF558E A Simple Task 解法
发现值域很小(字符串值域),考虑类似于计数排序的方法:统计区间内每种数的数量,然后按照数量覆盖。
// Problem: E. A Simple Task
// Contest: Codeforces - Codeforces Round 312 (Div. 2)
// URL: https://codeforces.com/problemset/problem/558/E
// Memory Limit: 512 MB
// Time Limit: 5000 ms
#include <stdio.h>
const int maxn = 1.03e5;
struct data {
int bucket[26];
char lazy;
data(char lazy_ = 0) : lazy(lazy_) { for(int i=0;i<26;i++) bucket[i]=0; }
}tree[maxn<<4];
data merge(data l, data r) {
data res;
for(int i=0;i<26;i++)
res.bucket[i] = l.bucket[i] + r.bucket[i];
return res;
}
void print(data x){
for(int i=0;i<26;i++)
if(x.bucket[i])
printf("[%c : %d] ", 'a'+i, x.bucket[i]);
}
void print_raw(data x){
for(int i=0;i<26;i++)
for(int j=0;j<x.bucket[i];j++)
putchar('a'+i);
}
void setlazy(int index, int l, int r, char lazy){
tree[index] = data();
tree[index].bucket[lazy-'a'] = r-l+1;
tree[index].lazy = lazy;
}
void pushlazy(int index, int l, int r) {
if(not tree[index].lazy) return;
int mid = (l+r)>>1;
setlazy(index<<1, l, mid, tree[index].lazy);
setlazy(index<<1|1, mid+1, r, tree[index].lazy);
tree[index].lazy = 0;
}
void fill(int index, int l, int r, int ql, int qr, char ch){
pushlazy(index, l, r);
if(ql <= l and r <= qr)
return setlazy(index, l, r, ch);
if(l > qr or r < ql)
return;
int mid = (l+r)>>1;
fill(index<<1, l, mid, ql, qr, ch);
fill(index<<1|1, mid+1, r, ql, qr, ch);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
data sum(int index, int l, int r, int ql, int qr){
pushlazy(index, l, r);
if(ql <= l and r <= qr)
return tree[index];
if(l > qr or r < ql)
return data();
int mid = (l+r)>>1;
return merge(sum(index<<1, l, mid, ql, qr), sum(index<<1|1, mid+1, r, ql, qr));
}
char ch;
void build(int index, int l, int r){
if(l == r) {
do{
ch=getchar();
} while(ch<'a' or 'z'<ch);
tree[index].bucket[ch-'a']++;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
void output(int index, int l, int r){
pushlazy(index, l, r);
if(l == r) {
print_raw(tree[index]);
return;
}
int mid = (l+r)>>1;
output(index<<1, l, mid);
output(index<<1|1, mid+1, r);
}
int n, m;
int u, v, w;
int main() {
scanf("%d%d", &n, &m);
build(1, 1, n);
for(int i=1; i<=m; i++) {
scanf("%d%d%d", &u, &v, &w);
data res = sum(1, 1, n, u, v);
if(w == 1) {
int r = u;
for(int i=0;i<26;i++)
if(res.bucket[i])
fill(1, 1, n, r, r+res.bucket[i]-1, 'a'+i),
r += res.bucket[i];
}
else{
int r = v;
for(int i=0;i<26;i++)
if(res.bucket[i])
fill(1, 1, n, r-res.bucket[i]+1, r, 'a'+i),
r -= res.bucket[i];
}
}
output(1, 1, n);puts("");
return 0;
}
CF240F TorCoder
请使用文件输入输出!
给定一个长为 的由 a 到 z 组成的字符串,有 次操作,每次操作将 这些位置的字符进行重排,得到字典序最小的回文字符串,如果无法操作就不进行。
求 次操作后的字符串。
CF240F TorCoder 解法
首先重排形成回文串的充要条件是有小于等于一种字符出现了奇数次。
然后剩下的就暴力覆盖就行了,和 CF558E 做法相同。
注意 ababa 优于 baaab。
// Problem: TorCoder
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF240F
// Memory Limit: 250 MB
// Time Limit: 3000 ms
#include <stdio.h>
const int maxn = 1.03e5;
bool ed;
struct data {
int bucket[26];
char lazy;
data(char lazy_ = 0) : lazy(lazy_) { for(int i=0;i<26;i++) bucket[i]=0; }
}tree[maxn<<4];
char ch;
int n, m, u, v, w;
bool bg;
data merge(data l, data r) {
data res;
for(int i=0;i<26;i++)
res.bucket[i] = l.bucket[i] + r.bucket[i];
return res;
}
void print(data x){
for(int i=0;i<26;i++)
if(x.bucket[i])
printf("[%c : %d] ", 'a'+i, x.bucket[i]);
}
void print_raw(data x){
for(int i=0;i<26;i++)
for(int j=0;j<x.bucket[i];j++)
putchar('a'+i);
}
void setlazy(int index, int l, int r, char lazy){
tree[index] = data();
tree[index].bucket[lazy-'a'] = r-l+1;
tree[index].lazy = lazy;
}
void pushlazy(int index, int l, int r) {
if(not tree[index].lazy) return;
int mid = (l+r)>>1;
setlazy(index<<1, l, mid, tree[index].lazy);
setlazy(index<<1|1, mid+1, r, tree[index].lazy);
tree[index].lazy = 0;
}
void fill(int index, int l, int r, int ql, int qr, char ch){
pushlazy(index, l, r);
if(ql <= l and r <= qr)
return setlazy(index, l, r, ch);
if(l > qr or r < ql)
return;
int mid = (l+r)>>1;
fill(index<<1, l, mid, ql, qr, ch);
fill(index<<1|1, mid+1, r, ql, qr, ch);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
data sum(int index, int l, int r, int ql, int qr){
pushlazy(index, l, r);
if(ql <= l and r <= qr)
return tree[index];
if(l > qr or r < ql)
return data();
int mid = (l+r)>>1;
return merge(sum(index<<1, l, mid, ql, qr), sum(index<<1|1, mid+1, r, ql, qr));
}
void build(int index, int l, int r){
if(l == r) {
do{
ch=getchar();
} while(ch<'a' or 'z'<ch);
tree[index].bucket[ch-'a']++;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
void output(int index, int l, int r){
pushlazy(index, l, r);
if(l == r) {
print_raw(tree[index]);
return;
}
int mid = (l+r)>>1;
output(index<<1, l, mid);
output(index<<1|1, mid+1, r);
}
int main() {
#ifdef debug_rickyxrc
fprintf(stderr, "Memory usage : %.4lf KB\n", (&ed-&bg) / 1024.0);
fprintf(stderr, "Memory usage : %.4lf MB\n", (&ed-&bg) / 1024.0 / 1024.0);
#else
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
scanf("%d%d", &n, &m);
build(1, 1, n);
for(int i=1; i<=m; i++) {
scanf("%d%d", &u, &v);
data res = sum(1, 1, n, u, v);
int odd=0, las=-1, l=u, r=v;
for(int i=0;i<26;i++) {
odd += res.bucket[i]&1;
if(res.bucket[i]&1)
las = i;
}
if(odd <= 1) {
for(int i=0;i<26;i++)
if(res.bucket[i])
fill(1, 1, n, l, l+(res.bucket[i]>>1)-1, 'a'+i), l += (res.bucket[i]>>1),
fill(1, 1, n, r-(res.bucket[i]>>1)+1, r, 'a'+i), r -= (res.bucket[i]>>1);
if(odd == 1)
fill(1, 1, n, l, l, 'a'+las);
}
}
output(1, 1, n);puts("");
return 0;
}
P3033 Cow Steeplechase G
给出 条平行于坐标轴的线段,要你选出尽量多的线段使得这些线段两两没有交点(顶点也算)。横的与横的,竖的与竖的线段之间保证没有交点,输出最多能选出多少条线段。
P3033 Cow Steeplechase G 解法
很小 ,且是约束问题,考虑网络流。
我们发现,每对相交的线段都应该被选在两个集合中,所以我们给线段建点,连边,跑最小割。
这相当于把线段划分到两个集合中,最后用总线段数减去最小割即可。
// Problem: P3033 [USACO11NOV] Cow Steeplechase G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3033
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
#define int long long
const int maxn = 2 * 2e6 + 5, maxm = 2 * 2e6 + 5, inf = 0x3f3f3f3f3f3f3f3f;
int n, m, tot=1, head[maxn], cur[maxn], ter[maxm], nxt[maxm], cap[maxm], dis[maxn];
void add(int u, int v, int w) { ter[++tot] = v, nxt[tot] = head[u], cap[tot] = w, head[u] = tot; }
void addedge(int u, int v, int w) { add(u, v, w) , add(v, u, 0); }
bool bfs(int s,int t) {
memset(dis, -1 , sizeof(dis));
std::queue<int> q;
q.push(s), dis[s] = 0, cur[s] = head[s];
while(!q.empty()) {
int fr = q.front(); q.pop();
for(int i = head[fr] ; i ; i = nxt[i]) {
int v = ter[i];
if(cap[i] && dis[v] == -1) {
dis[v] = dis[fr] + 1;
q.push(v);
cur[v] = head[v];
if(v==t)
return true;
}
}
}
return false;
}
int dfs(int u, int t, int flow) {
if(u == t) return flow;
int ans = 0;
for(int &i = cur[u] ; i && ans < flow ; i = nxt[i]) {
int v = ter[i];
if(cap[i] && dis[v] == dis[u] + 1) {
int x = dfs(v, t, std::min(cap[i], flow - ans));
if(!x) dis[x] = -1;
cap[i] -= x,cap[i^1] += x, ans += x;
}
}
return ans;
}
int dinic(int s, int t) {
int ans = 0, x;
while (bfs(s,t)) {
while(x = dfs(s,t,inf))
ans += x;
}
return ans;
}
int u, v, w, c, s=1, t=2;
int xx1[maxn], xx2[maxn], yy1[maxn], yy2[maxn], typ[maxn];
int linex(int i) { return 2+i; }
int liney(int i) { return 2+n+i; }
signed main() {
scanf("%lld", &n);
for(int i=1;i<=n;i++){
scanf("%d%d%d%d", xx1+i, yy1+i, xx2+i, yy2+i);
if(xx1[i] > xx2[i]) xx1[i] ^= xx2[i] ^= xx1[i] ^= xx2[i];
if(yy1[i] > yy2[i]) yy1[i] ^= yy2[i] ^= yy1[i] ^= yy2[i];
}
for(int i=1;i<=n;i++){
typ[i] = (xx1[i] == xx2[i]);
if(typ[i])
addedge(s, linex(i), 1);
else
addedge(liney(i), t, 1);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) {
if(i!=j and typ[i] == 1 and typ[j] == 0 and xx1[j] <= xx1[i] and xx1[i] <= xx2[j] and yy1[i] <= yy1[j] and yy1[j] <= yy2[i])
addedge(linex(i), liney(j), 1);
}
int ans = dinic(s, t);
printf("%lld\n", n-ans);
return 0;
}
P2579 沼泽鳄鱼
潘塔纳尔沼泽地号称世界上最大的一块湿地,它地位于巴西中部马托格罗索州的南部地区。每当雨季来临,这里碧波荡漾、生机盎然,引来不少游客。
为了让游玩更有情趣,人们在池塘的中央建设了几座石墩和石桥,每座石桥连接着两座石墩,且每两座石墩之间至多只有一座石桥。这个景点造好之后一直没敢对外开放,原因是池塘里有不少危险的食人鱼。
豆豆先生酷爱冒险,他一听说这个消息,立马赶到了池塘,想做第一个在桥上旅游的人。虽说豆豆爱冒险,但也不敢拿自己的性命开玩笑,于是他开始了仔细的实地勘察,并得到了一些惊人的结论:食人鱼的行进路线有周期性,这个周期只可能是 、 或者 个单位时间。每个单位时间里,食人鱼可以从一个石墩游到另一个石墩。每到一个石墩,如果上面有人它就会实施攻击,否则继续它的周期运动。如果没有到石墩,它是不会攻击人的。
借助先进的仪器,豆豆很快就摸清了所有食人鱼的运动规律,他要开始设计自己的行动路线了。每个单位时间里,他只可以沿着石桥从一个石墩走到另一个石墩,而不可以停在某座石墩上不动,因为站着不动还会有其它危险。如果豆豆和某条食人鱼在同一时刻到达了某座石墩,就会遭到食人鱼的袭击,他当然不希望发生这样的事情。
现在豆豆已经选好了两座石墩 和 ,他想从 出发,经过 个单位时间后恰好站在石墩 上。假设石墩可以重复经过(包括 和 ),他想请你帮忙算算,这样的路线共有多少种(当然不能遭到食人鱼的攻击)。
P2579 沼泽鳄鱼 解法
发现食人鱼的位置只有 种,对应的只有 种转移矩阵。
分别求出再跑快速幂即可。
// Problem: P2579 [ZJOI2005] 沼泽鳄鱼
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2579
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include<stdio.h>
#include<memory.h>
const int mod = 10000;
enum matrix_type{ null, basic };
template<const int maxn>
struct matrix {
int data[maxn][maxn];
matrix(matrix_type type = matrix_type::null){
if(type == matrix_type::null) memset(data, 0, sizeof data);
if(type == matrix_type::basic) for(int i=0;i<maxn;i++) data[i][i]=1;
}
int* operator[](int index) { return data[index]; }
};
template<const int n>
inline matrix<n> operator*(matrix<n> a, matrix<n> b){
matrix<n> res;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
for(int k=0;k<n;k++)
res[i][j] = (res[i][j] + 1ll * a[i][k] * b[k][j]) % mod;
return res;
}
template<const int n>
void excr(matrix<n>& mx, int point) { for(int i=0;i<n;i++) mx[i][point] = 0; }
const int maxn = 57;
matrix<maxn> gos[12], mulsum(matrix_type::basic), powsum(matrix_type::basic);
template<const int n>
matrix<n> pow(matrix<n> x, int p){
matrix<n> res(matrix_type::basic);
while(p){
if(p&1)
res = res * x;
x = x*x;
p>>=1;
}
return res;
}
int n, m, s, t, ed, k, u, v, nfish;
int main(){
scanf("%d%d%d%d%d", &n, &m, &s, &ed, &k);
for(int i=0;i<m;i++){
scanf("%d%d", &u, &v);
for(int j=0;j<12;j++)
gos[j][u][v] = gos[j][v][u] = 1;
}
scanf("%d", &nfish);
for(int k=0;k<nfish;k++){
scanf("%d", &t);
for(int j=0;j<t;j++) {
scanf("%d", &u);
for(int i=0;i+j-1<12;i+=t)
if(i+j-1>=0)
excr(gos[i+j-1], u);
}
}
for(int i=0;i<12;i++)
powsum = powsum * gos[i];
mulsum = pow(powsum, k/12);
for(int i=0;i<k%12;i++)
mulsum = mulsum * gos[i];
printf("%d\n", mulsum[s][ed]);
return 0;
}
CF1114F Please, another Queries on Array?
输入的第一行有两个数 ,保证 ,表示序列的长度以及询问的个数。
第二行是 个数 表示序列,满足 。
在接下来的 行,每行表示一个操作,其具体意义见题目描述。
保证数据中至少有一次操作 。
CF1114F Please, another Queries on Array? 解法
发现很重要的一个解题切入点:,那么我们发现 以内的质数有 个,不难想到状压。
然后 ,发现需要维护区间乘积和区间质因子。
第一项乘起来,第二项或一下就好。
// Problem: F. Please, another Queries on Array?
// Contest: Codeforces - Codeforces Round 538 (Div. 2)
// URL: https://codeforces.com/problemset/problem/1114/F
// Memory Limit: 256 MB
// Time Limit: 5500 ms
#include<stdio.h>
#include<vector>
void assert_val(bool val, char* failed) { if(not val) printf("%s FAILED.\n", failed); }
const int maxn = 2e6;
typedef long long i64;
template <const int mod> struct modint;
template <const int mod> modint<mod> pow(modint<mod> x, int p){
modint<mod> res(1);
while(p) {
if(p&1) res*=x;
x*=x; p>>=1;
}
return res;
}
template <const int mod> struct modint{
int x;
modint(int v=0){
if(v<0 or v>=mod) printf("modint::modint<%d>(%d:int) : Error : %d overflow.\n", mod, v, v);
this->x = v;
}
modint<mod> inv() const { return pow(*this, mod-2); }
};
template <const int mod> bool operator==(modint<mod> a, modint<mod> b) { return a.x==b.x; }
template <const int mod> const modint<mod> operator+(modint<mod> a, modint<mod> b) { return modint<mod>(a.x+b.x>=mod?a.x+b.x-mod:a.x+b.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a) { return a.x==0?0:modint<mod>(mod-a.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a, modint<mod> b) { return a + (-b); }
template <const int mod> const modint<mod> operator*(modint<mod> a, modint<mod> b) { return modint<mod>(1ll * a.x * b.x % mod); }
template <const int mod> const modint<mod> operator/(modint<mod> a, modint<mod> b) { return a * b.inv(); }
template <const int mod> const modint<mod> operator+=(modint<mod>& a, modint<mod> b) { return a = a+b; }
template <const int mod> const modint<mod> operator-=(modint<mod>& a, modint<mod> b) { return a = a-b; }
template <const int mod> const modint<mod> operator*=(modint<mod>& a, modint<mod> b) { return a = a*b; }
template <const int mod> const modint<mod> operator/=(modint<mod>& a, modint<mod> b) { return a = a/b; }
const int mod = 1000000007;
typedef modint<mod> mi;
std::vector<int> primes ={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101 ,103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293};
std::vector<mi> primes_mul;
i64 prime_down(int x) {
i64 res = 0; int i=0;
for(auto prime : primes)
res |= (1ll<<i) * (x % prime == 0), i++;
return res;
}
mi decomp(i64 x){
mi res = 1;
for(int b=63;b>=0;b--)
if((x>>b)&1)
res = res * primes_mul[b];
return res;
}
struct data {
mi dat;
i64 ors, orslazy;
mi lazy;
data(mi dat_ = mi(0), i64 ors_=0, mi lazy_=1, i64 lazyor_=0) : dat(dat_), ors(ors_), lazy(lazy_), orslazy(lazyor_) {}
} tree[maxn<<2];
void setlazy(int index, int l, int r, mi lazy, i64 ors) {
tree[index].dat *= pow(mi(lazy), r-l+1);
tree[index].lazy *= lazy;
tree[index].orslazy |= ors;
tree[index].ors |= ors;
}
void push(int index, int l, int r) {
if(tree[index].lazy == mi(1) and tree[index].orslazy == 0)
return;
assert_val(((tree[index].lazy == mi(1)) && (tree[index].orslazy == 0)) == 0, "push::lazy_exist");
int mid = (l+r)>>1;
setlazy(index<<1, l, mid, tree[index].lazy, tree[index].orslazy), setlazy(index<<1|1, mid+1, r, tree[index].lazy, tree[index].orslazy);
tree[index].lazy=1, tree[index].orslazy=0;
}
data merge(data l, data r) {
return data(
l.dat * r.dat,
l.ors | r.ors
);
}
void build(int index, int l, int r) {
if(l == r) {
int t;
scanf("%d", &t);
tree[index].dat = t;
tree[index].ors = prime_down(t);
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid);
build(index<<1|1, mid+1, r);
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
void mul(int index, int l, int r, int ql, int qr, int val, i64 pd) {
push(index, l, r);
if(ql <= l and r <= qr) return setlazy(index, l, r, val, pd);
if(l > qr or r < ql) return;
int mid = (l+r)>>1;
mul(index<<1, l, mid, ql, qr, val, pd), mul(index<<1|1, mid+1, r, ql, qr, val, pd);
assert_val(tree[index].orslazy == 0 and tree[index].lazy == mi(1), (char *)"mul::lazy_not_pushed");
tree[index] = merge(tree[index<<1], tree[index<<1|1]);
}
data query(int index, int l, int r, int ql, int qr) {
push(index, l, r);
if(ql <= l and r <= qr) return tree[index];
int mid = (l+r)>>1;
if(qr <= mid)
return query(index<<1, l, mid, ql, qr);
if(ql > mid)
return query(index<<1|1, mid+1, r, ql, qr);
return merge(query(index<<1, l, mid, ql, qr), query(index<<1|1, mid+1, r, ql, qr));
}
int n, m;
void prework() { for(auto prime:primes) primes_mul.push_back((mi(prime)-mi(1)) / mi(prime)); }
char s[20];
int u, v, w;
int main() {
prework();
scanf("%d%d", &n, &m);
build(1, 1, n);
for(int i=1;i<=m;i++) {
scanf("%s", s);
if(s[0] == 'T') {
scanf("%d%d", &u, &v);
data res = query(1, 1, n, u, v);
printf("%d\n", (res.dat * decomp(res.ors)).x);
}
else {
scanf("%d%d%d", &u, &v, &w);
mul(1, 1, n, u, v, w, prime_down(w));
}
}
return 0;
}
abc327_f apples
有几棵苹果树排在一条数线上,个苹果从树上掉下来。
具体地说,每一个 都有一个苹果在时间 落在坐标 处。
高桥有一个耐久度为、长度为的篮子,他可以做以下动作恰好一次。
选择正整数 和 。他在时将篮子放置在范围内,在时将其取回。他可以得到从放置篮子到取回篮子这段时间内掉落在篮子覆盖范围内的所有苹果。
篮子放好后,他不能移动篮子,篮子取回后,他也不能再放篮子。
求他能得到的苹果的最大数量。
abc327_f apples 解法
发现是在求长为 ,宽为 的矩形能框住的点的最大数量。
首先,当前的框在坐标 ,其覆盖的右上角为 。
这样的话位置要满足关于两个坐标轴的不等式,不太方便。
我们首先将第一维排序,用类似于扫描线的思路加入和删除,这样就变成了一个区间问题。
所以线段树要支持区间加和查询区间最大值。
// Problem: F - Apples
// Contest: AtCoder - HHKB Programming Contest 2023(AtCoder Beginner Contest 327)
// URL: https://atcoder.jp/contests/abc327/tasks/abc327_f
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
#include<stdio.h>
#include<vector>
const int maxn = 2.02e5;
const int maxl = 2e6;
int data[maxl<<2], maxv[maxl<<2], lazy[maxl<<2];
int max(int a, int b) { return a>b?a:b; }
void setlazy(int index, int l, int r, int v) { data[index] += v * (r-l+1), lazy[index] += v, maxv[index] += v; }
void push(int index, int l, int r) {
if(not lazy[index]) return;
int mid = (l+r)>>1;
setlazy(index<<1, l, mid, lazy[index]), setlazy(index<<1|1, mid+1, r, lazy[index]);
lazy[index]=0;
}
void modify(int index, int l, int r, int ql, int qr, int v) {
push(index, l, r);
if(ql <= l and r <= qr) return setlazy(index, l, r, v);
if(l > qr or r < ql) return;
int mid = (l+r)>>1;
modify(index<<1, l, mid, ql, qr, v), modify(index<<1|1, mid+1, r, ql, qr, v);
data[index] = data[index<<1] + data[index<<1|1];
maxv[index] = max(maxv[index<<1], maxv[index<<1|1]);
}
int n, d, w, x, y, res, xx;
std::vector<int> del[maxn], add[maxn];
int main() {
scanf("%d%d%d", &n, &d, &w);
for(int i=1;i<=n;i++)
scanf("%d%d", &x, &y),
xx = max(x-d+1, 1),
add[xx].push_back(y),
del[x+1].push_back(y);
for(int v=1;v<maxn;v++) {
for(auto u : add[v]) modify(1, 1, maxn, max(1, u-w+1), u, 1);
for(auto u : del[v]) modify(1, 1, maxn, max(1, u-w+1), u, -1);
res = max(res, maxv[1]);
}
printf("%d\n", res);
return 0;
}
P2012 拯救世界2
经过 12 年的韬光养晦,世界末日再次来临(众人:什么鬼逻辑…)。
这次,小a 和 uim 已经做好了一切准备,顺利召唤出了 kkksc03 大神和 lzn 大神。然而,kkksc03 和 lzn 告诉他们,这次世界末日太过强大,他们已无法挽回,只有创世神 JOHNKRAM 能拯救这个世界。
然而,创世神 JOHNKRAM 是无法召唤的,除非把整个宇宙按照 全部转化成能量。因为根据 C_SUNSHINE 大神随手推算出的召唤定律,至少需要被召唤者百万亿分之一的能量才能召唤(众人:什么鬼定律…)。
当然,还有一种方法,那就是找出创世神 JOHNKRAM 的基因序列。普通人基因序列由 A、C、G、T 构成,创世神 JOHNKRAM 不是普通人(是个胖纸),基因序列也不一样。除了这四种普通的,还有乾、兑、离、震、巽、坎、艮、坤八种特殊基因。其中乾、坎、艮、震属阳,只能出现奇数次;坤、兑、离、巽属阴,只能出现偶数次。
现在只知道创世神 JOHNKRAM 的基因序列共有 位,其他一概不知。小a 和 uim 想知道他们最多要试多少次,才能召唤出创世神 JOHNKRAM 。这个数字有可能很大,所以输出答案模 即可(C_SUNSHINE 的忠告:远离八卦,远离肥胖)。
P2012 拯救世界2 解法
校内有一道题的 idea,比这个弱,可惜最后没用。
这题原先想的 CRT 合并,后来发现复杂了。
相当于有 12 种不同的元素,其中四种只能用奇数次,四种只能用偶数次,另外四种没有限制。
发现 在 意义下没有乘法逆元,所以考虑转化。
在 时发现答案为 ,这题就做完了。
P4322 最佳团体
JSOI 信息学代表队一共有 名候选人,这些候选人从 到 编号。方便起见,JYY 的编号是 号。每个候选人都由一位编号比他小的候选人 推荐。如果 ,则说明这个候选人是 JYY 自己看上的。
为了保证团队的和谐,JYY 需要保证,如果招募了候选人 ,那么候选人 也一定需要在团队中。当然了,JYY 自己总是在团队里的。每一个候选人都有一个战斗值 ,也有一个招募费用 。JYY 希望招募 个候选人(JYY 自己不算),组成一个性价比最高的团队。也就是,这 个被 JYY 选择的候选人的总战斗值与总招募费用的比值最大。
P4322 最佳团体 解法
是分数规划问题,考虑二分。
然后就变成了在树上选择 个点每个点有依赖和价值,要求价值大于等于 (必须选)。
发现这个是一个树上背包的板子,然后暴力搞一下就行了,复杂度看起来是 的,但实际上只会统计每对点的贡献,复杂度是 的。
// Problem: #C. 最佳团体
// Contest: Hydro
// URL: [Removed]
// Memory Limit: 256 MB
// Time Limit: 1000 ms
#include<stdio.h>
#include<vector>
typedef long long i64;
typedef double f64;
const int maxn = 2512;
std::vector<int> edge[maxn];
double cost[maxn], val[maxn];
int k, n, fad;
double f[maxn][maxn]; // choose k
int siz[maxn];
void initsiz(int index, int fa) {
siz[index] = 1;
for(auto u : edge[index])
if(u != fa)
initsiz(u, index),
siz[index] += siz[u];
}
double max(double a, double b) { return a > b ? a : b; }
double min(double a, double b) { return a < b ? a : b; }
int min(int a, int b) { return a < b ? a : b; }
double midv;
double gval(int index) { return val[index] - midv * cost[index]; }
void dfs(int index, int fa) {
f[index][1] = gval(index);
for(auto u : edge[index])
if(u != fa) {
dfs(u, index);
for(int i = min(siz[index], k+1); i; i--)
for(int j = 0; j<=min(siz[u], i-1); j++)
f[index][i] = max(f[index][i], f[index][i-j] + f[u][j]);
}
}
bool check(double mid) {
for(int i=0;i<=n+5;i++)
for(int j=0;j<=k+5;j++)
f[i][j] = -1e20;
midv = mid;
dfs(0, -1);
return f[0][k+1] >= 0;
}
int main() {
scanf("%d%d", &k, &n);
for(int i=1;i<=n;i++) {
scanf("%lf%lf%d", cost+i, val+i, &fad);
edge[i].push_back(fad), edge[fad].push_back(i);
}
initsiz(0, -1);
f64 l = 0, r = 1.2e4;
while(r-l > 1e-4) {
f64 sum = l + r;
i64 v = (* (i64 *) & (sum)) - 0x10000000000000ll;
f64 mid = * (f64 *) &v; // 整了一下活
if(check(mid))
l = mid;
else
r = mid;
}
printf("%.3lf", l);
return 0;
}
abc187f Close Group
给定一个 个节点 条边的无向图,要求通过删去若干条边(可以不删),使得每个连通块都是完全图。求最少分成多少个连通块。
abc187f Close Group 解法
比幻想乡那题简单。
发现 极小,考虑状态压缩。
定义 代表二进制集合 的最小划分数,状态初始值应为:
中途的转移很简单:
最后从小到大二进制枚举子集即可,复杂度 。
popcount 函数出自 Earthmessenger的博客,拜谢大佬。
// Problem: [ABC187F] Close Group
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/AT_abc187_f
// Memory Limit: 1 MB
// Time Limit: 3000 ms
#include<stdio.h>
#include<vector>
inline int popcnt(unsigned int x)
{
x = ((x & 0xaaaaaaaa) >> 1 ) + (x & 0x55555555);
x = ((x & 0xcccccccc) >> 2 ) + (x & 0x33333333);
x = ((x & 0xf0f0f0f0) >> 4 ) + (x & 0x0f0f0f0f);
x = ((x & 0xff00ff00) >> 8 ) + (x & 0x00ff00ff);
x = ((x & 0xffff0000) >> 16) + (x & 0x0000ffff);
return x;
}
int full_graph(int x) { return x*(x-1)/2; }
int min(int a, int b) { return a<b?a:b; }
const int maxn = 21;
std::vector<int> edge[maxn];
int f[1<<maxn], d[1<<maxn], graph[1<<maxn];
int n, m, u, v;
int main() {
scanf("%d%d", &n, &m);
for(int i=1; i<=m; i++)
scanf("%d%d", &u, &v), u--, v--,
graph[(1<<u) | (1<<v)] ++;
for(int S=1; S<(1<<n); S++)
for(int T=S; T; T=(T-1)&S)
d[S] += graph[T];
for(int S=1; S<(1<<n); S++)
f[S] = (full_graph(popcnt(S)) == d[S]) ? 1 : 0x3f3f3f3f;
for(int S=1; S<(1<<n); S++)
for(int T=S; T; T=(T-1)&S)
f[S] = min(f[T] + f[S^T], f[S]);
printf("%d\n", f[(1<<n)-1]);
return 0;
}
abc324_f Beautiful Path
个点 条边的有向图,保证对于所有边,。每条边有两个属性 。找到一条 的路径,使得 的值最大。你的输出与答案的误差不得超过 。
abc324_f Beautiful Path 题解
是一个分数规划的板子。
二分答案,并在 DAG 上 dp 寻找最优解即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 7e5;
vector<std::pair<int,std::pair<int,int> > > edge[maxn];
int n,m,u,v,w1,w2;
double r[maxn];
std::queue<int> q;
bool check(double delta){
for(int i=1;i<=n;i++)
r[i]=-1e12;
r[1]=0;
for(int u=1;u<n;u++)
for(auto v:edge[u]) {
double vl = r[u]+(1.*v.second.first - delta*1.*v.second.second);
if(r[v.first] < vl)
r[v.first] = vl;
}
return r[n] >= 0;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++)
cin>>u>>v>>w1>>w2,
edge[u].push_back({v,{w1,w2}});
double l = 0,r = 2.3e9;
while(r-l>1e-10){
double mid = (l+r)/2.;
if(check(mid))
l=mid;
else
r=mid;
}
cout<<fixed<<setprecision(12)<<l<<endl;
return 0;
}
P3966 单词
小张最近在忙毕设,所以一直在读论文。一篇论文是由许多单词组成,但小张发现一个单词会在论文中出现很多次,他想知道每个单词分别在论文中出现了多少次。
P3966 单词 解法
据说这题被暴力搞过去了(
AC 自动机【加强版】的板子。
把所有串拼起来,中间加上 {({ - a = 27)然后再跑 AC 自动机就行。
// Problem: P3966 [TJOI2013] 单词
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3966
// Memory Limit: 500 MB
// Time Limit: 1000 ms
#include <bits/stdc++.h>
#include <string>
// #define maxn 8000001
const int maxn = 8.02e6;
using namespace std;
char s[maxn];
std::string res;
int n, cnt, vis[maxn], rev[maxn], indeg[maxn], ans;
struct trie_node
{
int son[28];
int fail;
int flag;
int ans;
void init()
{
memset(son, 0, sizeof(son));
fail = flag = 0;
}
} trie[maxn];
queue<int> q;
void init()
{
for (int i = 0; i <= cnt; i++)
trie[i].init();
for (int i = 1; i <= n; i++)
vis[i] = 0;
cnt = 1;
ans = 0;
}
void insert(char *s, int num)
{
int u = 1, len = strlen(s);
for (int i = 0; i < len; i++)
{
int v = s[i] - 'a';
if (!trie[u].son[v])
trie[u].son[v] = ++cnt;
u = trie[u].son[v];
}
if (!trie[u].flag)
trie[u].flag = num;
rev[num] = trie[u].flag;
return;
}
void getfail(void)
{
for (int i = 0; i < 27; i++)
trie[0].son[i] = 1;
q.push(1);
trie[1].fail = 0;
while (!q.empty())
{
int u = q.front();
q.pop();
int Fail = trie[u].fail;
for (int i = 0; i < 27; i++)
{
int v = trie[u].son[i];
if (!v)
{
trie[u].son[i] = trie[Fail].son[i];
continue;
}
trie[v].fail = trie[Fail].son[i];
indeg[trie[Fail].son[i]]++;
q.push(v);
}
}
}
void topu()
{
for (int i = 1; i <= cnt; i++)
if (!indeg[i])
q.push(i);
while (!q.empty())
{
int fr = q.front();
q.pop();
vis[trie[fr].flag] = trie[fr].ans;
int u = trie[fr].fail;
trie[u].ans += trie[fr].ans;
if (!(--indeg[u]))
q.push(u);
}
}
void query(const char *s)
{
int u = 1, len = strlen(s);
for (int i = 0; i < len; i++)
u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}
int main()
{
scanf("%d", &n);
init();
for (int i = 1; i <= n; i++)
scanf("%s", s),
res += s, res += '{',
insert(s, i);
getfail();
// scanf("%s", s);
query(res.c_str());
topu();
for (int i = 1; i <= n; i++)
cout << vis[rev[i]] << std::endl;
return 0;
}
P3121 Censoring G
FJ 把杂志上所有的文章摘抄了下来并把它变成了一个长度不超过 的字符串 。他有一个包含 个单词的列表,列表里的 个单词记为 。他希望从 中删除这些单词。
FJ 每次在 中找到最早出现的列表中的单词(最早出现指该单词的开始位置最小),然后从 中删除这个单词。他重复这个操作直到 中没有列表里的单词为止。注意删除一个单词后可能会导致 中出现另一个列表中的单词。
FJ 注意到列表中的单词不会出现一个单词是另一个单词子串的情况,这意味着每个列表中的单词在 中出现的开始位置是互不相同的。
请帮助 FJ 完成这些操作并输出最后的 。
P3121 Censoring G 题解
// Problem: P3121 [USACO15FEB] Censoring G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3121
// Memory Limit: 256 MB
// Time Limit: 1000 ms
#include <stdio.h>
#include <queue>
#include <string.h>
#include <stack>
const int maxn = 100007;
const int maxs = 27;
char runn[maxn];
int trie[maxn][maxs], fail[maxn], val[maxn], cnt, wordlen[maxn];
int mp(char c) { return c - 'a'; }
void insert(char *c, int len)
{
int index = 0;
for (int i = 0; i < len; i++)
{
if (!trie[index][mp(c[i])]) trie[index][mp(c[i])] = ++cnt;
index = trie[index][mp(c[i])];
}
val[index]++;
wordlen[index] = len;
return;
}
void build_fail()
{
std::queue<int> q;
for (int i = 0; i < 26; i++)
if (trie[0][i])
q.push(trie[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
if (trie[u][i])
fail[trie[u][i]] = trie[fail[u]][i],
q.push(trie[u][i]);
else
trie[u][i] = trie[fail[u]][i];
}
}
int n;
char ch[maxn];
std::stack<char> str, res;
std::stack<int> ptr;
void run() {
for(int i=0, index=0, e = strlen(runn); i<e; i++) {
index = trie[index][mp(runn[i])];
str.push(runn[i]), ptr.push(index);
if(wordlen[index]) {
for(int j=0;j<wordlen[index];j++)
str.pop(), ptr.pop();
index = ptr.top();
}
}
}
int main()
{
ptr.push(0);
scanf("%s", runn);
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%s", ch),
insert(ch, strlen(ch));
build_fail();
run();
while(not str.empty())
res.push(str.top()), str.pop();
while(not res.empty())
putchar(res.top()), res.pop();
return 0;
}
P2444 病毒
二进制病毒审查委员会最近发现了如下的规律:某些确定的二进制串是病毒的代码。如果某段代码中不存在任何一段病毒代码,那么我们就称这段代码是安全的。现在委员会已经找出了所有的病毒代码段,试问,是否存在一个无限长的安全的二进制代码。
示例:
例如如果 为病毒代码段,那么一个可能的无限长安全代码就是 。如果 为病毒代码段,那么就不存在一个无限长的安全代码。
现在给出所有的病毒代码段,判断是否存在无限长的安全代码。
P2444 病毒
正难则反,如果有一段无限长的安全代码,那么将它放在 AC 自动机上跑,一定能跑进一个没有危险标记的环。
反之亦然,所以我们通过 dfs 找出根节点可以到达的一个没有危险标记的环即可。
注意:一个节点的 fail 若危险,则它也危险(fail 是最长后缀)。
// Problem: P2444 [POI2000] 病毒
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2444
// Memory Limit: 125 MB
// Time Limit: 1000 ms
#include <stdio.h>
#include <queue>
#include <string.h>
#define maxn 1000000
#define maxs 3
int trie[maxn][maxs], fail[maxn], val[maxn], cnt;
int mp(char c) { return c - '0'; }
void insert(char *c, int len)
{
int index = 0;
for (int i = 0; i < len; i++)
{
if (!trie[index][mp(c[i])])
trie[index][mp(c[i])] = ++cnt;
index = trie[index][mp(c[i])];
}
val[index]=1;
return;
}
void build_fail()
{
std::queue<int> q;
for (int i = 0; i < 2; i++)
if (trie[0][i])
q.push(trie[0][i]);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int i = 0; i < 2; i++)
if (trie[u][i]) {
fail[trie[u][i]] = trie[fail[u]][i];
q.push(trie[u][i]);
val[trie[u][i]] |= val[fail[trie[u][i]]];
}
else
trie[u][i] = trie[fail[u]][i];
}
}
int n;
char ch[maxn];
int vis[maxn];
bool infinite(int index) {
if(vis[index]== 1) return true;
if(vis[index]==-1) return false;
vis[index] = 1;
for(int i=0;i < 2;i++) {
if((not val[trie[index][i]]) and infinite(trie[index][i]))
return true;
}
vis[index]=-1;
return false;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%s", ch), insert(ch, strlen(ch));
build_fail();
puts(infinite(0) ? "TAK" : "NIE");
return 0;
}
UVA 11019 Matrix Matcher
组数据,每组数据给定一个 的 矩阵,满足 ,再给定一个 的 矩阵,满足 ,求 矩阵在 矩阵中出现的次数。
UVA 11019 Matrix Matcher 解法
// Problem: Matrix Matcher
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11019
// Memory Limit: 0 MB
// Time Limit: 3000 ms
#include<stdio.h>
#include<ctype.h>
inline int min(int a, int b) { return a<b?a:b; }
inline int max(int a, int b) { return a>b?a:b; }
template <const int mod> struct modint;
template <const int mod> modint<mod> pow(modint<mod> x, int p){
modint<mod> res(1);
while(p){
if(p&1)
res*=x;
x*=x;
p>>=1;
}
return res;
}
template <const int mod> struct modint{
int x;
modint(int v=0){
#ifdef debug_rickyxrc
if(v<0 or v>=mod)
printf("modint::modint<%d>(%d:int) : Error : %d overflow.\n", mod, v, v);
#endif
this->x = v;
}
modint<mod> inv() const { return pow(*this, mod-2); }
};
template <const int mod> bool operator==(modint<mod> a, modint<mod> b) { return a.x==b.x; }
template <const int mod> const modint<mod> operator+(modint<mod> a, modint<mod> b) { return modint<mod>(a.x+b.x>=mod?a.x+b.x-mod:a.x+b.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a) { return a.x==0?0:modint<mod>(mod-a.x); }
template <const int mod> const modint<mod> operator-(modint<mod> a, modint<mod> b) { return a + (-b); }
template <const int mod> const modint<mod> operator*(modint<mod> a, modint<mod> b) { return modint<mod>(1ll * a.x * b.x % mod); }
template <const int mod> const modint<mod> operator/(modint<mod> a, modint<mod> b) { return a * b.inv(); }
template <const int mod> const modint<mod> operator+=(modint<mod>& a, modint<mod> b) { return a = a+b; }
template <const int mod> const modint<mod> operator-=(modint<mod>& a, modint<mod> b) { return a = a-b; }
template <const int mod> const modint<mod> operator*=(modint<mod>& a, modint<mod> b) { return a = a*b; }
template <const int mod> const modint<mod> operator/=(modint<mod>& a, modint<mod> b) { return a = a/b; }
template <const int mod1, const int mod2> struct double_modint {
modint<mod1> x1;
modint<mod2> x2;
double_modint(int v1=0) : x1(v1), x2(v1) {}
double_modint(modint<mod1> v1, modint<mod2> v2) : x1(v1), x2(v2) {}
double_modint<mod1, mod2> inv() const{
return double_modint<mod1, mod2>(x1.inv(), x2.inv());
}
};
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator+ (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1+b.x1, a.x2+b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator- (double_modint<mod1, mod2> a) { return double_modint<mod1, mod2>(-a.x1, -a.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator- (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1-b.x1, a.x2-b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator* (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1*b.x1, a.x2*b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator/ (double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return double_modint<mod1, mod2>(a.x1/b.x1, a.x2/b.x2); }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator+= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a+b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator-= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a-b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator*= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a*b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> operator/= (double_modint<mod1, mod2>& a, double_modint<mod1, mod2> b) { return a=a/b; }
template <const int mod1, const int mod2> double_modint<mod1, mod2> pow(double_modint<mod1, mod2> x, int p) { return double_modint<mod1, mod2>(pow<mod1> (x.x1, p), pow<mod2> (x.x2, p)); }
template <const int mod1, const int mod2> bool operator==(double_modint<mod1, mod2> a, double_modint<mod1, mod2> b) { return (a.x1==b.x1) and (a.x2==b.x2);}
const int mod1 = 998244353, mod2 = 998244853;
using hashval = double_modint<mod1, mod2>;
#ifndef debug_rickyxrc
const hashval p1 = 387, p2 = 961;
#else
const hashval p1 = 3, p2 = 7;
#endif
bool edmem;
const int maxn = 1007;
hashval hashn[maxn][maxn], hashsub[maxn][maxn];
int n, m, w, h;
int mp[maxn][maxn], mp2[maxn][maxn];
hashval powp1[maxn], powp2[maxn];
bool bgmem;
struct point {
int i, j;
point(int i_=0, int j_=0) : i(i_), j(j_) {}
};
inline point operator+(point a, point b) { return point(a.i+b.i, a.j+b.j); }
inline point operator-(point a) { return point(-a.i, -a.j); }
inline point operator-(point a, point b) { return a + (-b); }
template <class T> inline T getv(T vals[][maxn], point p1) { /*printf("(%d, %d) = %d\n", p1.i, p1.j, vals[p1.i][p1.j]); */return vals[p1.i][p1.j]; }
template <class T> inline T directsum(T vals[][maxn], point p1, point p2) {
T res = getv(vals, p2);
res -= getv(vals, point(p1.i-1, p2.j));
res -= getv(vals, point(p2.i, p1.j-1));
res += getv(vals, p1 - point(1, 1));
return res;
}
template <class T> inline void getsum(T vals[][maxn], int s1, int s2){
for(int i=1;i<=s1;i++)
for(int j=1;j<=s2;j++)
vals[i][j] += vals[i-1][j] + vals[i][j-1] - vals[i-1][j-1];
}
inline hashval directhash(hashval vals[][maxn], point a, point b) {
return directsum(vals, a, b) * powp1[a.i-1] * powp2[a.j-1];
}
inline int readi()
{
char c=getchar();int x=0;bool f=0;
for(;!isdigit(c);c=getchar())f^=!(c^45);
for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;return x;
}
int T;
char ch;
int main() {
#ifndef debug_rickyxrc
#else
fprintf(stderr, "Memory usage : %.4lf KB\n", (&edmem-&bgmem) / 1024.0),
fprintf(stderr, "Memory usage : %.4lf MB\n", (&edmem-&bgmem) / 1024.0 / 1024.0),
fprintf(stderr, "Memory usage : %.4lf GB\n", (&edmem-&bgmem) / 1024.0 / 1024.0 / 1024.0);
#endif
powp1[0] = powp2[0] = 1;
const hashval p1i = p1.inv(), p2i = p2.inv();
for(int i=1; i<maxn; i++)
powp1[i] = powp1[i-1] * p1i,
powp2[i] = powp2[i-1] * p2i;
scanf("%d", &T);
while(T--) {
n = readi(), m = readi();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
do {
ch = getchar();
} while(ch<'a' or 'z'<ch);
mp[i][j] = ch-'a'+1;
}
w = readi(), h = readi();
for(int i=1;i<=w;i++)
for(int j=1;j<=h;j++){
do {
ch = getchar();
} while(ch<'a' or 'z'<ch);
mp2[i][j] = ch-'a'+1;
}
hashval x = 1, y = 1;
for(int i=1;i<=n;i++, x*=p1) { y = 1;
for(int j=1;j<=m;j++, y*=p2)
hashn [i][j] = hashval(getv(mp , point(i, j))) * x * y;
}
x = 1, y = 1;
for(int i=1;i<=w;i++, x*=p1) { y = 1;
for(int j=1;j<=h;j++, y*=p2)
hashsub[i][j] = hashval(getv(mp2, point(i, j))) * x * y;
}
getsum(hashn , n, m);
getsum(hashsub, w, h);
int ans = 0;
for(int i=1;i<=n-w+1;i++)
for(int j=1;j<=m-h+1;j++)
ans += directhash(hashn, point(i, j), point(i+w-1, j+h-1)) == hashsub[w][h];
printf("%d\n", ans);
}
return 0;
}
P4735 最大异或和
给定一个非负整数序列 ,初始长度为 。
有 个操作,有以下两种操作类型:
A x:添加操作,表示在序列末尾添加一个数 ,序列的长度 加 。Q l r x:询问操作,你需要找到一个位置 ,满足 ,使得: 最大,输出最大值。
P4735 最大异或和 解法
首先我们将区间异或值转化为前缀差分数组上的异或元素对。
然后就可以用可持久化 0-1 Trie 维护,具体地,用版本号维护右端点,在对于每个节点,维护它的最右侧的下标(所属的版本号)。
这样就可以用查询最大异或值的方式来做,保证当前版本号大于等于左区间版本号即可。
// Problem: P4735 最大异或和
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4735
// Memory Limit: 512 MB
// Time Limit: 1500 ms
#include<stdio.h>
const int maxn = 2e7;
#ifdef debug_rickyxrc
const int maxl = 3;
#else
const int maxl = 31;
#endif
int max(int a, int b) { return a > b ? a : b; }
int sons[maxn][2], path[maxn], cnt;
int copy_node(int index) {
sons[++cnt][0] = sons[index][0];
sons[ cnt][1] = sons[index][1];
path[cnt] = path[index];
return cnt;
}
int new_node() { return ++cnt; }
int vers[maxn], vcnt;
void ins(int root, int x, int ind) {
int index = copy_node(root);
vers[++vcnt] = index;
for(int b= maxl; b>=0; b--) {
path[index] = max(path[index], ind);
sons[index][x>>b&1] = copy_node(sons[index][x>>b&1]);
index = sons[index][x>>b&1];
}
path[index] = max(path[index], ind);
}
int n, m, u, v, w;
char q;
int querymax(int l, int r, int x) {
int index = vers[r], res = 0;
for(int b= maxl; b>=0; b--) {
int v = (x>>b)&1;
if(sons[index][v^1] and path[sons[index][v^1]]>=l) index = sons[index][v^1], res += (1ll << b);
else index = sons[index][v];
}
return res;
}
int las, l;
int main () {
vcnt=-1;ins(0, 0, 0);
scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++) scanf("%d", &u), l = u, u ^= las, las^= l, ins(vers[vcnt], u, i);
for(int i=1;i<=m;i++) {
do { q = getchar(); } while(q!='A' and q!='Q');
if(q == 'A')
scanf("%d", &u), l = u, u ^= las, las^= l,
ins(vers[vcnt], u, ++n);
else
scanf("%d%d%d", &u, &v, &w), u--, v--,
printf("%d\n", querymax(u, v, w^las));
}
return 0;
}
P6279 Favorite Colors G
Farmer John 的 头奶牛每头都有一种最喜欢的颜色。奶牛们的编号为 ,每种颜色也可以用 中的一个整数表示。
存在 对奶牛 ,奶牛 仰慕奶牛 。有可能 ,此时一头奶牛仰慕她自己。对于任意颜色 ,如果奶牛 和 都仰慕一头喜欢颜色 的奶牛,那么 和 喜欢的颜色相同。
给定这些信息,求一种奶牛喜欢颜色的分配方案,使得每头奶牛最喜欢的颜色中不同颜色的数量最大。由于存在多种符合这一性质的分配方案,输出字典序最小的(这意味着你应当依次最小化分配给奶牛 的颜色)。
P6279 Favorite Colors G 做法
我觉得这题挺神的。
反向建图,那么每个点的出边指向的点都是颜色相同的,考虑合并,最后一直合并直到无法再次合并。
那么我们需要在每次合并时合并两个点的出边,每次将小的并到大的里面,然后用一个点来作为这两个点的代表元素。(说白了就是启发式合并)
#include<stdio.h>
#include<vector>
#include<queue>
const int maxn = 2.02e5;
std::vector<int> edge[maxn];
int fas[maxn], size[maxn], res[maxn], cnt;
std::queue<int> qu;
void init(int n) { for(int i=1;i<=n;i++) fas[i] = i, size[i] = 1; }
int findf(int index) {
if(fas[index] == index)
return index;
return findf(fas[index]);
}
int merge(int i, int j) {
auto ii = findf(i), jj = findf(j);
if(ii == jj) return ii;
if(size[ii] < size[jj]) {
fas[ii] = jj, size[jj] += size[ii];
for(auto v : edge[ii]) edge[jj].push_back(v); edge[ii].clear();
return jj;
}
fas[jj] = ii, size[ii] += size[jj];
for(auto v : edge[jj]) edge[ii].push_back(v); edge[jj].clear();
return ii;
}
int n, m, u, v;
int main() {
scanf("%d%d", &n, &m);
init(n);
for(int i=1;i<=m;i++)
scanf("%d%d", &v, &u),
edge[v].push_back(u);
for(int i=1;i<=n;i++)
qu.push(i);
while(not qu.empty()) {
int u = findf(qu.front()); qu.pop();
if(edge[u].size() < 2) continue;
int f = edge[u][0];
for(int i=1; i<edge[u].size(); i++) f = merge(f, edge[u][i]);
edge[u].clear(); edge[u].push_back(f); qu.push(f);
}
for(int i=1;i<=n;i++) {
int j = findf(i);
res[j] = res[j] ? res[j] : ++cnt;
printf("%d\n", res[j]);
}
return 0;
}
P2824 排序
在 年,佳媛姐姐喜欢上了数字序列。因而她经常研究关于序列的一些奇奇怪怪的问题,现在她在研究一个难题,需要你来帮助她。
这个难题是这样子的:给出一个 到 的排列,现在对这个排列序列进行 次局部排序,排序分为两种:
0 l r表示将区间 的数字升序排序1 l r表示将区间 的数字降序排序
注意,这里是对下标在区间 内的数排序。
最后询问第 位置上的数字。
P2824 排序 做法
挺神的。
发现对数列局部排序不方便,但是如果数列值域很小(如 0-1 数列),就可以采用 A simple Task 那道题的方法,用区间覆盖代替排序,将复杂度降到
我们现在就转化序列,二分答案。
每次我们判断答案是否大于等于 k,具体地,数列 ,对这个数列排序,最后检验 是否为 即可。
#include<stdio.h>
#include<vector>
const int maxn = 2.02e5;
struct data {
int bucket[2] = {0, 0}, lazy = 0, lf = 0;
} tree[maxn<<2];
int li[maxn], n, m, u, v, t, qpos;
std::vector<std::pair<int, std::pair<int, int>>> qu;
void setlazy(int index, int l, int r ,int v) {
tree[index].lf = 1;
tree[index].lazy = v;
tree[index].bucket[v] = r-l+1;
tree[index].bucket[v^1] = 0;
}
void pushlazy(int index, int l, int r) {
if(tree[index].lf == 0) return;
int mid = (l+r)>>1;
setlazy(index<<1, l, mid, tree[index].lazy), setlazy(index<<1|1, mid+1, r, tree[index].lazy);
tree[index].lf = 0;
}
void build(int index, int l, int r, int qval) {
tree[index].lazy = tree[index].lf = 0;
if(l == r) {
tree[index].bucket[li[l]>=qval] = 1,
tree[index].bucket[li[l] <qval] = 0;
return;
}
int mid = (l+r)>>1;
build(index<<1, l, mid, qval), build(index<<1|1, mid+1, r, qval);
for(int b=0;b<=1;b++)
tree[index].bucket[b] = tree[index<<1].bucket[b] + tree[index<<1|1].bucket[b];
}
std::pair<int, int> operator+ (std::pair<int, int> a, std::pair<int, int> b) { return {a.first+b.first, a.second+b.second};}
int get(std::pair<int,int> s, int p) { return p ? s.second : s.first; }
std::pair<int, int> querysum(int index, int l, int r, int ql, int qr) {
pushlazy(index, l, r);
if(ql <= l and r <= qr)
return {tree[index].bucket[0], tree[index].bucket[1]};
if(l > qr or r < ql)
return {0, 0};
int mid = (l+r)>>1;
return querysum(index<<1, l, mid, ql, qr) + querysum(index<<1|1, mid+1, r, ql, qr);
}
void fill(int index, int l, int r, int ql, int qr, int qval) {
pushlazy(index, l, r);
if(ql <= l and r <= qr) {
return setlazy(index, l, r, qval);
}
if(l > qr or r < ql)
return;
int mid = (l+r)>>1;
fill(index<<1, l, mid, ql, qr, qval), fill(index<<1|1, mid+1, r, ql, qr, qval);
for(int b=0;b<=1;b++)
tree[index].bucket[b] = tree[index<<1].bucket[b] + tree[index<<1|1].bucket[b];
}
bool ans_ge_n(int qval) {
build(1, 1, n, qval);
for(int i=1;i<=m;i++) {
auto ans = querysum(1, 1, n, qu[i].second.first, qu[i].second.second);
fill(1, 1, n, qu[i].second.first, qu[i].second.first+get(ans, qu[i].first)-1, qu[i].first);
fill(1, 1, n, qu[i].second.first+get(ans, qu[i].first), qu[i].second.first+ans.first+ans.second-1, qu[i].first^1);
}
return querysum(1, 1, n, qpos, qpos).second;
}
int main() {
scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++)
scanf("%d", li+i);
qu.push_back({0, {0, 0}});
for(int i=1;i<=m;i++)
scanf("%d%d%d", &t, &u, &v),
qu.push_back({t, {u, v}});
scanf("%d", &qpos);
int l = 1, r = n, ans = -1;
while(l <= r) {
int mid = (l+r)>>1;
if(ans_ge_n(mid))
ans = mid, l = mid+1;
else
r = mid-1;
}
printf("%d", ans);
return 0;
}
P4198 楼房重建
小 A 的楼房外有一大片施工工地,工地上有 栋待建的楼房。每天,这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆,数自己能够看到多少栋房子。
为了简化问题,我们考虑这些事件发生在一个二维平面上。小 A 在平面上 点的位置,第 栋楼房可以用一条连接 和 的线段表示,其中 为第 栋楼房的高度。如果这栋楼房上任何一个高度大于 的点与 的连线没有与之前的线段相交,那么这栋楼房就被认为是可见的。
施工队的建造总共进行了 天。初始时,所有楼房都还没有开始建造,它们的高度均为 。在第 天,建筑队将会将横坐标为 的房屋的高度变为 (高度可以比原来大—修建,也可以比原来小—拆除,甚至可以保持不变—建筑队这天什么事也没做)。请你帮小 A 数数每天在建筑队完工之后,他能看到多少栋楼房?
P4198 楼房重建 解法
好题,之前某道校内赛的题也是这种思路。
将楼房看作斜率,发现我们在找从 开始的最长上升子序列。
那么我们考虑如何用线段树维护这个。
发现这个区间不好合并,所以我们要在 pushup 时进行线段树上二分。
具体如何二分呢?考虑被看到区间的首项和最大值都要被选中,然后按照这个线段树二分即可。
如果写分数类,记得初始化为 ,被这个卡了很久很久。
#include<stdio.h>
const int maxn = 100007;
struct frac {
int x=1, y;
operator double() {
if(x == 0)
return 0;
return 1.*y/x;
}
};
bool operator> (frac a, frac b) { return 1ll*a.y*b.x > 1ll*b.y*a.x; }
bool operator< (frac a, frac b) { return b > a; }
bool operator==(frac a, frac b) { return 1ll * a.y * b.x == 1ll * b.y * a.x; }
bool operator<=(frac a, frac b) { return !(a>b); }
bool operator>=(frac a, frac b) { return !(a<b); }
frac max(frac a, frac b) { return a > b ? a : b; }
struct data { int num; frac mxfrc; } tree[maxn<<2];
frac frcs[maxn];
void pushup(int index) { tree[index].mxfrc = max(tree[index<<1].mxfrc, tree[index<<1|1].mxfrc); }
int pushup2(frac required_min, int index, int l, int r) {
if(tree[index].mxfrc <= required_min) { return 0; }
if(frcs[l] > required_min) { return tree[index].num; }
if(l==r) { return frcs[l] > required_min; }
int mid = (l+r)>>1;
if(tree[index<<1].mxfrc <= required_min) return pushup2(required_min, index<<1|1, mid+1, r);
else return pushup2(required_min, index<<1, l, mid) + tree[index].num - tree[index<<1].num;
}
void modify(int index, int l, int r, int q, int v) {
if(q <= l and r <= q)
return void(tree[index] = {1, {q, v}});
int mid = (l+r)>>1;
if(q <= mid) modify(index<<1, l, mid, q, v);
else modify(index<<1|1, mid+1, r, q, v);
pushup(index), tree[index].num = tree[index<<1].num + pushup2(tree[index<<1].mxfrc, index<<1|1, mid+1, r);
}
int n, m, u ,v;
int main() {
scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++)
frcs[i] = {i, 0};
for(int i=1;i<=m;i++)
scanf("%d%d", &u, &v),
frcs[u] = {u, v},
modify(1, 1, n, u, v),
printf("%d\n", tree[1].num);
return 0;
}
UVA1434 YAPTCHA
求出下列式子的答案:( 已经手动修补)
UVA1434 YAPTCHA 做法
好早就做过这题了,复习一下。
根据威尔逊定理:
通过类似的方式可以证明 不是质数时答案为 (太懒了呜呜呜)。
所以线性筛出质数即可。
#include<stdio.h>
const int maxn = 4e6;
char check[maxn]; int prime[maxn], cnt, psum[maxn];
void euler() {
for(int i=2;i<maxn;i++) {
if(not check[i]) prime[++cnt] = i;
for(int j=1;j<=cnt and 1ll*i*prime[j] < maxn;j++) {
check[i*prime[j]] = 1;
if(i % prime[j] == 0) break;
}
}
for(int i=2;i<=1e6+2;i++)
psum[i] = !check[3*i+7] + psum[i-1];
}
int T, u;
int main() {
euler();
scanf("%d", &T);
while(T--) {
scanf("%d", &u);
printf("%d\n", psum[u]);
}
return 0;
}
P4139 上帝与集合的正确用法
定义 ,可以证明 在某一项后都是同一个值,求这个值。
P4139 上帝与集合的正确用法 做法
我们定义 ,现在需要求出 。
发现这个式子是递归的,接下来证明式子的时间复杂度。
最后一个快速幂一个线性筛 就完了,尽管我用的是手动求
#include<stdio.h>
int phi(int n) {
int res = n;
for(int i=2; i*i<=n; i++)
if(n % i == 0) {
res = res / i * (i-1);
while( n % i == 0 ) n /= i;
}
if(n > 1) res = res /n *(n-1);
return res;
}
int pow(int x, int p, int mod) {
int res = 1;
while(p) {
if(p&1)
res = 1ll * res * x % mod;
x = 1ll * x * x % mod, p>>=1;
}
return res;
}
int f(int x) {
if(x==1) return 0; int p = phi(x);
return pow(2, f(p)+p, x);
}
int T, u;
int main() {
scanf("%d", &T);
while(T--) {
scanf("%d", &u);
printf("%d\n", f(u));
}
return 0;
}
P4211 LCA
给出一个 个节点的有根树(编号为 到 ,根节点为 )。
一个点的深度定义为这个节点到根的距离 。
设 表示点 的深度, 表示 与 的最近公共祖先。
有 次询问,每次询问给出 ,求 。
P4211 LCA 做法
妈的考场上想到了没时间了妈的妈的妈的
分拆贡献,发现可以将深度拆为根节点到每个选中节点上的路径加 。
于是问题就在于快速选中节点。
不难想到离线询问,前缀和求解即可。
#include <stdio.h>
#include <vector>
#define maxn 1000007
#define int long long
int n, m, r, lis[maxn], lisid[maxn], u, v;
const int p = 201314;
namespace treecutpf
{
std::vector<int> edge[maxn];
int fa[maxn], size[maxn], depth[maxn], hson[maxn], top[maxn], id[maxn], rev[maxn], dfn;
void dfs(int index, int fath)
{
fa[index] = fath;
size[index] = 1;
depth[index] = depth[fath] + 1;
for (auto u : edge[index])
if (u != fath)
{
dfs(u, index);
size[index] += size[u];
if (size[hson[index]] < size[u])
hson[index] = u;
}
}
void treecut(int index, int topp)
{
id[index] = ++dfn;
rev[dfn] = index;
top[index] = topp;
if (!hson[index])
return;
treecut(hson[index], topp);
for (auto u : edge[index])
if (u != fa[index] && u != hson[index])
treecut(u, u);
}
}
using namespace treecutpf;
namespace segtree
{
#define ls (index << 1)
#define rs (ls | 1)
#define mid ((l + r) >> 1)
#define nseq index, l, r
#define lseq ls, l, mid
#define rseq rs, mid + 1, r
int data[maxn << 2], lazy[maxn << 2];
void setlazy(int index, int l, int r, int val)
{
data[index] += ((r - l + 1) * val) % p;
lazy[index] += val % p;
}
void pushlazy(int index, int l, int r)
{
lazy[index] %= p;
setlazy(lseq, lazy[index]);
setlazy(rseq, lazy[index]);
lazy[index] = 0;
}
void update(int index)
{
data[ls] %= p;
data[rs] %= p;
data[index] = (data[ls] + data[rs]) % p;
}
void init(int index, int l, int r, int *vals)
{
if (l == r)
{
data[index] = vals[l] % p;
return;
}
init(lseq, vals);
init(rseq, vals);
update(index);
}
void add(int ql, int qr, int val, int index, int l, int r)
{
if (qr < ql)
return add(qr, ql, val, index, l, r);
pushlazy(nseq);
if (ql <= l && r <= qr)
{
setlazy(nseq, val % p);
return;
}
if (l > qr || r < ql)
return;
add(ql, qr, val % p, lseq);
add(ql, qr, val % p, rseq);
update(index);
}
int query(int ql, int qr, int index, int l, int r)
{
if (qr < ql)
return query(qr, ql, index, l, r);
pushlazy(nseq);
if (ql <= l && r <= qr)
return data[index] % p;
if (l > qr || r < ql)
return 0;
return (query(ql, qr, lseq) + query(ql, qr, rseq)) % p;
}
}
using namespace segtree;
namespace treeopt
{
int querypath(int u, int v)
{
int res = 0;
while (top[u] != top[v])
if (depth[top[u]] > depth[top[v]])
res = (res + query(id[u], id[top[u]], 1, 1, n)) % p,
u = fa[top[u]];
else
res = (res + query(id[v], id[top[v]], 1, 1, n)) % p,
v = fa[top[v]];
res = (res + query(id[u], id[v], 1, 1, n)) % p;
return res;
}
void modifypath(int u, int v, int val)
{
while (top[u] != top[v])
if (depth[top[u]] > depth[top[v]])
add(id[u], id[top[u]], val % p, 1, 1, n),
u = fa[top[u]];
else
add(id[v], id[top[v]], val % p, 1, 1, n),
v = fa[top[v]];
add(id[u], id[v], val, 1, 1, n);
}
}
using namespace treeopt;
std::vector<std::pair<int, std::pair<int, int>>> queries[maxn];
int qans[maxn], w;
signed main()
{
scanf("%lld%lld", &n, &m);
for(int i=1;i<n;i++)
scanf("%lld", &u), u++,
edge[i+1].push_back(u),
edge[u].push_back(i+1);
r=1;
dfs(r, r);
treecut(r, r);
for(int i=1;i<=m;i++)
scanf("%lld%lld%lld", &u, &v, &w), u++, v++, w++,
queries[u-1].push_back({w, {i, p-1}}),
queries[v] .push_back({w, {i, 1}});
for(int i=1;i<=n;i++) {
modifypath(1, i, 1);
for(auto query: queries[i])
qans[query.second.first] = (qans[query.second.first] + 1ll * query.second.second * querypath(1, query.first) % p) % p;
}
for(int i=1;i<=m;i++)
printf("%lld\n", qans[i]);
}